SOLUTION: what is the equation fot the circle with a center of (-4,-7) and tangent to x=2?

To get the equation of a circle we need the center (h,k)
and the radius r, and the standard equation for a circle




We have the center point, so all we need is the radius.

Let's plot the center (-4,-7) and draw the line  which is
a vertical line through 2 on the x-axis, shown in green below:

 

We draw a horizontal line from the center over to where the
circle is to be tangent to the green line, for that will be a
radius for the circle, which we can also draw in::



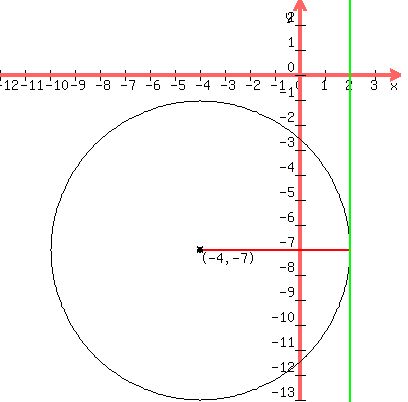Using the x-axis as a measuring stick, we can see that that radius
is 6 units long, 4 units over to the y-axis and 2 units more on the
right side of the y-axis, which makes the radius 6 units long.  So
all that's left to do is substitute (h,k)= (-4,-7), and r=6 into the 
standard equation for a circle:




That's it.

Edwin