SOLUTION: If P is the any point on the hyperbola whose axis are equal,prove that SP.SP'=CP^2. please explain it completely.

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: If P is the any point on the hyperbola whose axis are equal,prove that SP.SP'=CP^2. please explain it completely.      Log On


   

Question 252347: If P is the any point on the hyperbola whose axis are equal,prove that SP.SP'=CP^2. please explain it completely.
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
If P is the any point on the hyperbola whose axis are equal,prove that SP%2AS%27P=CP%5E2, where S and S' are the foci, and C is the center.


Let the tranverse axis be along the x-axis and the conjugate axis be
along the y-axis, with the center C at (0,0), the origin.

Let both axes be 2, so that both the semi-tranverse axis, "a", and 
semi-conjugate axis, "b", are 1 each.   Then the equation of the 
hyperbola, which is x%5E2%2Fa%5E2-y%5E2%2Fb%5E2=1, becomes simply x%5E2-y%5E2=1.
In a hyperbola, c%5E2=a%5E2%2Bb%5E2, so c%5E2=1%5E2%2B1%5E2=1%2B1=2, therefore
c+=+sqrt%282%29, where "c" is the distance from the center to the focus.
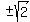Therefore S and S' are the points (%22%22%2B-sqrt%282%29,0).  

[Do not confuse the center "C(0,0)" with the value of "c", the distance 
from the center to each focus.]

Let P(x,y) be any arbitrary point on the hyperbola:
The blue line is CP:

The graph is:

 

Using the distance formula to find SP and SP' in terms of x:



Since the equation of the hyperbola is x%5E2-y%5E2=1, then y%5E2=x%5E2-1,
so substituting we get:



SP+=+sqrt%28x%5E2-2x%2Asqrt%282%29%2B2%2Bx%5E2-1%29=+sqrt%282x%5E2-2x%2Asqrt%282%29%2B1%29

Similarly,



As before, since the equation of the hyperbola is x%5E2-y%5E2=1,
then y%5E2=x%5E2-1, so substituting we get:





So 




      
Multiplying under the radicals:





Next we use the distance formuls to find CP where C is the origin (0,0).

CP+=+sqrt%28%28x-0%29%5E2%2B%28y-0%29%5E2%29=sqrt%28x%5E2%2By%5E2%29

Since the equation of the hyperbola is x%5E2-y%5E2=1, then y%5E2=x%5E2-1,
so substituting we get

CP+=sqrt%28x%5E2%2By%5E2%29=sqrt%28x%5E2%2Bx%5E2-1%29=+sqrt%282x%5E2-1%29

so CP%5E2+=+%28sqrt%282x%5E2-1%29%29%5E2+=+abs%282x%5E2-1%29

Therefore SP%2A%22SP%27%22+=+CP%5E2, because both equal abs%282x%5E2-1%29 

Edwin