SOLUTION: find the coordinates of the point of intersection of the axis and the directrix of the parabola whose focus is (3,3) and directrix is 3x-4y=2.find also the length of the latus rect

We plot the focus and draw the directrix:



The axis of the parabola is a line perpendicular to the
directrix which passes through the focus and vertex of
the parabola.  

We will draw in the axis of the parabola (in green): 



We find the equation of the axis of the
parabola.

The slope of the directrix is found by solving its equation
for y, getting it in the form :





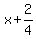
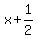So the slope of the directrix is 

So the slope of the vertex is its negative reciprocal


So to find the equation of the axis of the parabola, we
use  which becomes



and since it must go through (3,3), we substitute that
and get






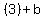
So the equation of the parabola's axis is 

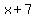, or multiplying through
by 3,
, or


So to find the point where they intersect, we
solve the system:



and get the point (,),
which in decimal form is .

This is the first answer you were asked to find.

----------------------------------------------

The distance from the focus to the vertex equals the
distance from the vertex to the directrix, and this
distance is the parabolic constant p.

Therefore the distance from the focus to the directrix
is 



To find this distance 2p, we use the distance formula:



with , , , ,   



Since , 

Let'as sketch in the parabola with the vertex
halfway between the focus and the directrix:



The latus rectum is the line segment parallel to the
directrix with ends on the parabola and which passes
through the focus, which is its midpoint.  We draw it
in:



Since every point on a parabola is the same distance from the
focus as it is to the directrix, the distance from the ends of
the latus rectum to the focus = 2p, and so the the length of the 
latus rectum is 4p, so the other answer to your problem is

length of the latus rectum = .

Edwin