|
Question 249616: Find the vertices and asymptotes of the hyperbola given by
x^2/25-y^2/2^2=1
(x squared over 25 minus y squared over 2 squared equals 1)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! The forms of equations of hyperbolas which tell us what we need are:
 (horizontally-oriented hyperbolas) (horizontally-oriented hyperbolas)
and
 (vertically-oriented hyperbolas) (vertically-oriented hyperbolas)
Fortunately, once we figure out that  and and  , we find that our equation is already in the desired form: , we find that our equation is already in the desired form:

This tells us that
h = 0
k = 0
 which means a = 5 which means a = 5
 which means b = 2 which means b = 2
From this information and the equation  we can find c: we can find c:



Before we start using the above to solve the problem, let's review what a, b and c represent:- For ellipses and hyperbolas, "a" represents the distance from the center to the vertices on the major axis
- For hyperbolas "b" is used to help find the slopes of the asymptotes for the hyperbola. For horizontally-oriented hyperbolas, the slopes are +-b/a and for vertically-oriented hyperbolas the slopes are +- a/b
- For ellipses and hyperbolas, "c" represents the distance from the center the the foci (on the major axis)
Center.
For an equation in one of the desired forms, the center is (h, k). So our center is (0,0). Since a, b and c are distances from the center, we need the center even though the problem does not ask for it.
Vertices on the major axis.
These are a distance of "a" from the center along the major axis. The major axis for this ellipse is horizontal so the vertices will be "a" units to the left and right of the center:
(0+5, 0) and (0-5, 0)
or
(5, 0) and (-5, 0)
Foci.
These are a distance of "c" from the center along the major axis. The major axis for this ellipse is horizontal so the vertices will be "c" units to the left and right of the center:
(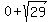 , 0) and ( , 0) and ( , 0) , 0)
Asymptotes.
First we need the slopes of the asymptotes. For horizontally-oriented hyperbolas the slopes are +- b/a. So the slopes for this hyperbola are:
+- 
The asymptotes pass through the center of the hyperbola so we want equations of lines that pass through the center, (0, 0), and have slopes of 2/5 and -2/5. There are a variety of ways to find such equations. One way is to use the Point-Slope form: 
For m = 2/5 and the point (0, 0) this becomes:

which simplifies to

For m = -2/5 and the point (0, 0) we get:

|
|
|
| |