|
Question 23528: A ship is monitoring the movement of a pod of whales with its radar. The radar screen can be modelled as a coordinate grid with the ship at the centre (0,0). The pod appears to be moving along a curve such that the absolute value of the difference of its distances from (2,7) and (2,-3) is always 6. Write an equation in standard form of hyperbola to describe the path of pod.
So far I got... the centre at (2,2) and 6/2 = 3^2 = 9
And the equation: x-2/a^2 - y-2/9 =1 I can't figure out (a
Answer by Paul(988)   (Show Source):
You can put this solution on YOUR website! Since now you know your new centre which is (2,2) and your a absolute value the equation goes like this: 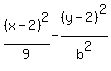 all you have now to do is to find the absolute value for b.
since you know that the transverse axis is 6 ---> 6/2=3^2 = 9 (a value)
The centre is (h-a,k) and (h+a,k)
(6-2,2) and (6+2,2) -> the distance between these two points is 4 (b value)
Since 3^2 = 9 (b)
4^2=16 (a)
Now pulg the terms into the equation.
Hence, the equation for the hyperbola is 
|
|
|
| |
