|
Question 227212: for the ellipse with equation 5x^2 + 64y^2 + 30x + 128y - 211=0,find the coordinates of the center,foci,and vertices.then graph the equation
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
The first part, transforming this into the proper form, is the hardest. The form for an ellipse is either:
 or
We start by "completing the square" for x and y:
1. Move the constant term to the other side (by adding 211):
2. Rearrange the terms, gathering the x terms and y terms:
3. Factor out the leading coefficient of the squared terms:
4. Use the perfect square pattern(s) to determine what we need to create perfect square trinomials. The perfect square patterns are:  and  . What we need to figure out is the  . And in order to do this we will need a value for "b". We find "b" by matching the first degree term with the pattern. For the x's the first degree term is 6x. We want it to match the 2ab pattern. With "a" being "x" the "b" would have to be "3" in order to match the pattern. This makes the  for the x terms. Using similar logic on the y terms we find that "b" and are 1.
So we want the left side of our equation to be:
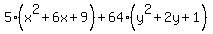
In order to add a 9 inside the parentheses for the x terms, we would need to add 5*9 to both sides of the equation (because of the 5 outside of the parentheses). Similarly we would need to add 64*1 to each side to add a 1 inside the parentheses for the y terms. (This is probably the hardest step of all to see.) So to create the perfect squares we need, we will add both 5*9 (45) and 64*1 (64) to both sides:
Simplifying and rewriting the perfect square trinomials as binomial squares:
5. Next we'll get the 1 we want on the right side by dividing both sides by 320:
Simplifying we get:
6. Rewrite, if necessary, the binomial squares as subtractions:
And we finally have the proper form for an ellipse!
From this equation we can see h, k,  and . h = -3 and k = -1. And  so  and  so  . We can also figure out  because in an ellipse  :
Now we can use h, k, a, b and c to find the center, vertices and the foci. Since the was under the x, this is a horizontally oriented ellipse and:
Center: (h, k)
Vertices on the major axis: (h + a, k) and (h - a, k)
Vertices on the minor axis: (h, k + b) and (h, k - b)
Foci: (h + c, k) and (h - c, k)
Substituting our h, k, a, b and c into these we get:
Center: (-3, -1)
Vertices on the major axis: (-3 + 8, -1) and (-3 - 8 , -1) or (5, -1) and (-11, -1)
Vertices on the minor axis: (-3, -1 +  ) and (-3, -1 - )
Foci: (-3 +  ), -1) and (-3 - ), -1)
To graph this ellipse:- Replace the square roots above with decimals from your calculator.
- Simplify the coordinates where you replaced the square roots.
- Plot and label the 4 vertices.
- "Connect the dots" of the four vertices into the shape of an ellipse.
- Plot and label the center and foci.
I'll leave the graphing up to you.
|
|
|
| |
