Question 176043: Circle with diameter which has endpoints at (-4,4) and (-8, 2)
Answer by EMStelley(208)   (Show Source):
You can put this solution on YOUR website! Since you know the endpoints of the diameter of the circle, you can find the midpoint of those two points, which would be the center of the circle, and you can find the radius by either halving the distance between the two points, or calculating the distance between one of the points and the center. Let's start by finding the center: we'll need the midpoint for this. If you have two points (a,b) and (c,d), the midpoint is
((a+c)/2, (b+d)/2)
So the midpoint between (-4,4) and (-8,2) is
((-4-8)/2, (4+2)/2) = (-6,3)
So the center of the circle is (-6,3). Now we need to find the radius. Let's do this by finding the distance between (-4,4) and (-6,3). Remember, the distance between two points (a,b) and (c,d) is:
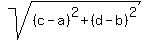
So, the distance between (-4,4) and (-6,3) is
So the radius of the circle is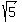 
Now that we have the center of the circle and the radius, we can write the equation for the circle, which is
 where (h,k) is the center, and r is the radius. So our circle's equation is
|
|
|
