|
Question 173643: Find the vertices, the endpoints of the minor axis, and the foci of the ellipse.
x^2+12x+36y^2-216y+324=0
Answer by gonzo(654)   (Show Source):
You can put this solution on YOUR website! your problem equation is:
this is the same as:
-----
what we did was group the x's and y's together and made the x^2 and the y^2 stand alone. this was in preparation for the next step.
-----
the next step is to complete the squares.
-----
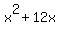 completes the square by taking 1/2 the 12 and taking the square of (x+6).
 .
to complete the square, we need to subtract 36.
what we get is:
we had to subtract the 36 because and we started with only 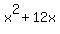 , so if we didn't subtract the 36 we would have been 36 over.
-----
we do the same for the y part of the equation.
we take 1/2 of the 6 and take the square of (y-3).
that becomes}
we had to subtract the 324 because  and we started with only  , so if we didn't subtract the 324 we would have been 324 over.
-----
our original equation was:
----
our modified equation becomes:
-----
combining like terms, this becomes:
add 36 to both sides of the equation and we get:
divide both sides of the equation by 36 and we get:
-----
this is now in the standard form of an elliptic equation which is:
where:
h is the x coordinate of the center of the ellipse.
k is the y coordinate of the center of the ellipse.
a is the distance from the center of the ellipse to the intersection of the ellipse along the major axis in both directions.
b is the distance from the center of the ellipse to the intersection of the ellipse along the minor axis.
the major axis in this case is the x axis.
the minor axis in this case is the y axis.
-----
we have enough information now to answer the questions.
the questions are:
Find the vertices, the endpoints of the minor axis, and the foci of the ellipse.
-----
the center of the ellipse is at (h,k) which becomes (-6,3)
this is because:
x-h = x+6, so -h = 6 which means h = -6.
y-k = y-3, so -k = -3 which means k = 3.
-----
since a^2 = 36, then a = 6 which is the distance along the major axis from the center of the ellipse to the ellipse in both directions (plus or minus).
-----
this makes the vertices of the ellipse at -12, and at 0 (plus or minus 6 from -6) since the vertices of the ellipse are the intersection of the ellipse with the major axis.
-----
since the major axis is on the line y = 3, the coordinates of the vertices of the ellipse are at:
(-12,3), and (0,3)
-----
since b^2 = 1, then b = 1 which is the distance along the minor axis from the center of the ellipse to the ellipse in both directions (plus or minus).
-----
this makes the endpoints of the minor axis of the ellipse at 2, and at 4 (plus or minus 1 from 3) since the endpoints of the minor axis are the intersection of the ellipse with the minor axis.
-----
since the minor axis is on the line x = -6, the coordinates of the endpoints of the minor axis are are at:
(-6,2) and (-6,4)
-----
what is left is to find the focus points.
-----
these are given by the equation:
c^2 = a^2 - b^2 (a is always greater than b)
-----
the equation becomes:
c^2 = (6)^2 - (1)^2 = 36 - 1 = 35
this makes
-----
c is the distance from the center of ellipse to the focus points (plus or minus).
the focus points are on the major axis which is the x axis.
this makes the focus points  and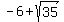 
which becomes approximately -11.9160, and -.0839.
this is the x value of that point.
since the major axis is on the line y = 3, then the coordinates of these points are at:
(-11.9160,3) and (-.0839,3)
-----
i truncated the values here, but used the full values in any calculations.
-----
to prove the equation for the ellipse was good, i had to prove that i could take any point on the ellipse at random, and the distance of that point to one of the focus points plus the distance of that point to the other focus point would equal to the length of the major axis.
-----
the length of the major axis of the ellipse is 2 * a which is 2 * 6 = 12.
-----
i took the point (0,3) as my test case.
when you see the graph you'll see that this point is on the ellipse.
the distance of this point to one of the focus points plus the distance of this point to the other focus point must = 12 for the ellipse equation to be good.
-----
the first focus point is:
(-11.9160,3)
distance from that to (0,3) is:
the second focus point is:
(-.0839,3)
the distance from that to (0,3) is:
-----
11.916 + .0839 = 11.999 = 12 (i used the full value in the calculator and got 12).
-----
this proves the equation for the ellipse is good.
-----
a graph of the ellipse is shown below.
you can see that the center is at (-6,3) and that the major axis intercepts the ellipse at (-12,3) and (0,3) since the major axis is on the line y = 3, and that the minor axis intercepts the ellipse at (-6,2) and (-6,4) since the minor axis is on the line x = -6.
the focus points are not shown the graph.
-----
the answer to your problem, in summary are:
vertices (endpoints of major axis) are (-12,3) and (0,3)
endpoints of minor axix are (-6,2) and (-6,4)
the focus points (lie on major axis) are (-11.9160,3) and (-.0839,3)
-----
a fairly decent tutorial on the subject can be found at the following web address:
http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_conics_ellipse.xml
-----
|
|
|
| |
