SOLUTION: one of my questions read,given the following info, write the standard equation for each conic. 1. Ellipse with a foci (-2,0) and (2,0) and verticies (-6,0) and(6,0)

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: one of my questions read,given the following info, write the standard equation for each conic. 1. Ellipse with a foci (-2,0) and (2,0) and verticies (-6,0) and(6,0)      Log On


   

Question 170283: one of my questions read,given the following info, write the standard equation for each conic.
1. Ellipse with a foci (-2,0) and (2,0) and verticies (-6,0) and(6,0)
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Remember, the standard equation for any ellipse is %28%28x-h%29%5E2%29%2F%28a%5E2%29%2B%28%28y-k%29%5E2%29%2F%28b%5E2%29=1


Also, the foci of any ellipse will lie on the major axis.

Since EVERY point given to you has a y-coordinate of 0, this means that the major axis lies horizontally. So this tells us that the length of the major axis is 2a (since "a" corresponds with the horizontal axis)


Finding the center:


To find the center, simply average the vertices to get


x-mid: %28-6%2B6%29%2F2=0%2F2=0

So the x-coordinate of the center is 0 which means that h=0



y-mid: %280%2B0%29%2F2=0%2F2=0

So the 0-coordinate of the center is 0 which means that k=0


So the center is (0,0) which tells us that h=0 and k=0


-------------------------------------------------------------------


Finding the length of the Major Axis:


Now let's find the distance from the two vertices:


Distance: d=sqrt%28%28-6-6%29%5E2%2B%280-0%29%5E2%29=sqrt%28%28-12%29%5E2%2B0%5E2%29=sqrt%28144%29=12


So the distance between the two vertices is 12 units (note: you can just count the units in between by use of a graph). This means that the length of the major axis is 12 units.


So this means that 2a=12 which tells us that a=6



-------------------------------------------------------------------


Finding the length of the Minor Axis:


To find the length of the minor axis (ie find the value of "b"), we first need to find the distance from the center to either focus

That distance is

Distance: d=sqrt%28%280-2%29%5E2%2B%280-0%29%5E2%29=sqrt%28%28-2%29%5E2%2B%280%29%5E2%29=sqrt%284%29=2


So the distance from the center to either focus is 2 units. This means that c=2


Now the value of "b" can be found through the formula


a%5E2=b%5E2%2Bc%5E2


6%5E2=b%5E2%2B2%5E2 Plug in a=6 and c=2


36=b%5E2%2B4 Square each value.


36-4=b%5E2 Subtract 4 from both sides.


b%5E2=32 Subtract and rearrange the equation.


b=sqrt%2832%29 Take the square root of both sides. Note: only the positive square root is considered


b=4%2Asqrt%282%29 Simplify the square root.



=========================================================


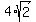So the values we've found was h=0, k=0, a=6, and b=4%2Asqrt%282%29


%28%28x-h%29%5E2%29%2F%28a%5E2%29%2B%28%28y-k%29%5E2%29%2F%28b%5E2%29=1 Go back to the general equation of an ellipse


%28%28x-0%29%5E2%29%2F%286%5E2%29%2B%28%28y-0%29%5E2%29%2F%28%284%2Asqrt%282%29%29%5E2%29=1 Plug in h=0, k=0, a=6, and b=4%2Asqrt%282%29



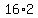
%28%28x-0%29%5E2%29%2F%2836%29%2B%28%28y-0%29%5E2%29%2F%2816%2A2%29=1 Square 6 to get 36. Square 4%2Asqrt%282%29 to get 16%2A2


%28%28x-0%29%5E2%29%2F%2836%29%2B%28%28y-0%29%5E2%29%2F%2832%29=1 Multiply


%28x%5E2%29%2F%2836%29%2B%28y%5E2%29%2F%2832%29=1 Simplify


====================================================

Answer:



So the equation of the ellipse with foci of (-2,0) and (2,0) and vertices (-6,0) and(6,0) is %28x%5E2%29%2F%2836%29%2B%28y%5E2%29%2F%2832%29=1