|
Question 170163: List all Applicable Information for the conic given in standard form. If the information isn't needed for the conic, write N/A. Show Work. (We have to graph it, but i dont think we can graph on this website. I just wanted to check if my graph was right with your answers.)

Center:
Covertices:
Focus or Foci:
Asymptopes:
Major Axis:
Transverse Axis:
Directrix:
Vertices/Vertex:
Radius:
Eccentricity:
Minor Axis:
Conjugate Axis:
Axis of Symmetry:
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Yes we can graph on here!
 We recognize this as an ellipse because the coefficients of
We recognize this as an ellipse because the coefficients of
 and and  when on the same side of the
equation are both positive and unequal. Also the coefficient
of when on the same side of the
equation are both positive and unequal. Also the coefficient
of  is smaller than the coefficient of is smaller than the coefficient of  .
So the graph will looks like the number 0 (zero). That is,
its major axis will be vertical.
We must get it in the standard form: .
So the graph will looks like the number 0 (zero). That is,
its major axis will be vertical.
We must get it in the standard form:
 Factor 36 out of the first two terms on the left,
and factor 25 out of the last two terms on the
left:
Factor 36 out of the first two terms on the left,
and factor 25 out of the last two terms on the
left:
 Multiply the coefficient of x, which is -8,
by
Multiply the coefficient of x, which is -8,
by  , getting , getting  . Then square . Then square
 and get and get 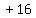 . Add . Add 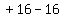 ,
which amounts to adding zero, inside the first
parentheses: ,
which amounts to adding zero, inside the first
parentheses:
 Multiply the coefficient of y, which is -6,
by
Multiply the coefficient of y, which is -6,
by  , getting , getting  . Then square . Then square
 and get and get 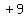 . Add . Add 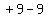 ,
which amounts to adding zero, inside the second
parentheses: ,
which amounts to adding zero, inside the second
parentheses:
 Group the first three terms in each parentheses
and factor:
Group the first three terms in each parentheses
and factor:

 Write the factorizations as squares of binomials:
Write the factorizations as squares of binomials:
 Distribute the 36 and the 25 into the outer
sets of parentheses, leaving the squares of
binomials intact:
Distribute the 36 and the 25 into the outer
sets of parentheses, leaving the squares of
binomials intact:




 Get a 1 on the right by dividing every term
by 900:
Get a 1 on the right by dividing every term
by 900:

 Comparing this to the form
Comparing this to the form
 We see that
We see that
 So the center is the point (h,k) = (4,3)
Let's plot the center (4,3):
So the center is the point (h,k) = (4,3)
Let's plot the center (4,3):
 Now since the ellipse's major axis is vertical, and since a = 6,
draw a vertical line from the center extending 6 units upward,
which will put it end at the point (4,9). That will be one of
the vertices.
Now since the ellipse's major axis is vertical, and since a = 6,
draw a vertical line from the center extending 6 units upward,
which will put it end at the point (4,9). That will be one of
the vertices.
 Also draw another vertical line from the center extending 6 units
downward, which will put its end at the point (4,-3) which will be
the other vertex.
Also draw another vertical line from the center extending 6 units
downward, which will put its end at the point (4,-3) which will be
the other vertex.
 since b = 5, draw a horizontal line from the center extending 5 units to the
right, which will put its end at the point (9,3). That will be one of
the covertices.
since b = 5, draw a horizontal line from the center extending 5 units to the
right, which will put its end at the point (9,3). That will be one of
the covertices.
 Also draw a horizontal line from the center extending 5 units to the
left, which will put its end at the point (-1,3). That will be the
other covertex:
Also draw a horizontal line from the center extending 5 units to the
left, which will put its end at the point (-1,3). That will be the
other covertex:
 Now we can sketch in the graph, approximately:
Now we can sketch in the graph, approximately:
 )}}}
We need to find the foci:
These are located
)}}}
We need to find the foci:
These are located  units from the center on the major
axis, where units from the center on the major
axis, where  .
So we calculate .
So we calculate  : :




 So the foci are the points:
So the foci are the points:
 The eccentricity is given by the formula
The eccentricity is given by the formula 

 You may not have studied that ellipses have
two directrices. Anyway, for an ellipse elongated
vertically the equations of the two directrices
of the ellipse is given by the equation
You may not have studied that ellipses have
two directrices. Anyway, for an ellipse elongated
vertically the equations of the two directrices
of the ellipse is given by the equation

 I won't draw these, since they are horizontal lines
both off the graph shown.
Center:
I won't draw these, since they are horizontal lines
both off the graph shown.
Center:  Covertices:
Covertices: 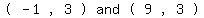 Focus or Foci:
Focus or Foci:  Asymptopes:
Asymptopes:  N/A
Major Axis: N/A
Major Axis:  Transverse Axis:
Transverse Axis: 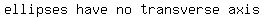 N/A
Directrix: If you've studied directrices of ellipse, they are N/A
Directrix: If you've studied directrices of ellipse, they are
 Vertices/Vertex:
Vertices/Vertex: 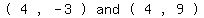 Radius:
Radius: 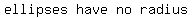 N/A
Eccentricity: N/A
Eccentricity:  Minor Axis:
Minor Axis:  Conjugate Axis:
Conjugate Axis: 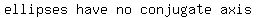 N/A
Axis of Symmetry: There are two axes of symmetry. The horizontal axis of
symmetry is the line y=3 and the vertical line of
symmetry is the line x=4.
Edwin N/A
Axis of Symmetry: There are two axes of symmetry. The horizontal axis of
symmetry is the line y=3 and the vertical line of
symmetry is the line x=4.
Edwin
|
|
|
| |