SOLUTION: Write an equation in standard form for: 1. An ellipse with center a the origin, one vertex at (0,5) and one co-vertex at (0,2). 2. A parabola with vertex at the origin and di

 
Draw those points: 
 

 
It is impossible to have a standard ellipse with a vertex and a 
co-vertex both on the y-axis.  So you have copied one of those 
points backward. I'll first assume the vertex should have been 
(5,0) instead of (0,5). Then we have this graph:
 


It is now easy to sketch in an ellipse with one vertex (5,0) and a co-vertex (0,2), as you see:



This ellipse is elongated horizontally like an egg resting on a 
table top.  Such an ellipse has the equation:



where 

(, ) is the center,

, and

, 

So in your problem, using (h,k) = (0,0)

 becomes




 
-------------------------------------

Next I'll assume the co-vertex should have been (2,0) 
instead of (0,2). Then we have this graph instead:
 


As you see, it is also easy to sketch in an ellipse with one vertex
(0,5) and a co-vertex (2,0):



This ellipse is elongated vertically like the character zero "0".  It
has this equation:



[Notice that  is under the term in  and that
 is under the term in , which was the other
way around in the case above. It is always true, though,
that  and  are always greater than 
and  respectively.]
 
where 

(, ) is the center,

, and

, 

So in interpreting your problem this way, we have,
again using (h,k) = (0,0),:

 becomes




 
-------------------------------------

2. A parabola with vertex at the origin and directrix y=-2


Such a parabola has equation:

 where the vertex is (, ).

Since this parabola has vertex (,), it has this
equation




We mark the origin and draw the directrix, in green, which is given as a
horizontal line 2 units below and parallel to the x-axis.



The vertex is 2 units ABOVE the directrix.  That's 2 units upward,
so therefore p = 2.  ---(If the vertex had been BELOW the directrix, we would have used p = -2)

Since the directrix is always entirely OUTSIDE the parabola,
we know that the parabola opens upward like this:



So since p=2 the equation of the parabola is







If you need the focus, (or focal point), it is a
point inside the parabola which is just as far from
the vertex as the directrix, but on the inside of
the parabola.  In other words, the focus (or focal
point) is (0,2) as you see in the graph below. Since
you asked about 'directrix' and 'foci' in one of the 
other problems, you have to understand focus (or focal point).
I did not mention the focus in the ellipse problems.  Perhaps
I should have.  All conics have at least one focal
point and a directrix.



---------------------------------

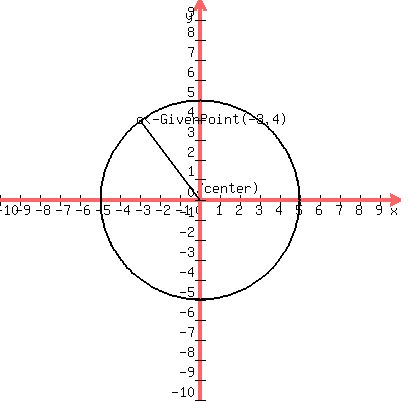
A circle with center (0,0) passing through (-3,4). 

First we'll draw it.  We draw the center and the point(-3,4):



Next we draw the radius from (0,0) to (-3,4)




Then we get a compass and draw the circle:



The equation of a circle with center (h,k) and radius r is



We know that the center is (0,0), so this becomes



We can find the radius either by using the distance formula


=
=
=
=

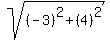or an easier way would be to have plugged (x,y)=(-3.4) into the
equation:








So the equation



becomes



or



---------------------------------------------

Hyperbola with vertices (8,-4) and (8,4) and foci (8,-6) and (8,6).

Let's draw those points:



The center of a hyperbola is the point midway between
the two vertices, which is also the point midway between 
the two foci.  So the center of the hyperbola is (8,0), so
we plot it:



The value of  is the distance from the center to a vertex.
The distance between (8,0) and the vertex (8,4) is 4 units, so 

The value of  is the distance from the center to a focus.
The distance between (8,0) and the vertex (8,6) is 6 units, so 

Now there is a Pythagorean relationship hyperbolas, that is,



Substituting:





 approximately.

Draw horizontal line segments through each vertex,
both right and left of each vertex, each equaling
to 

 
 
Now complete the defining rectangle for the hyperbola:

 

Draw the extended diagonals of that rectangle:



Draw in the hyperbola:



Hyperbolas which open up and down have this equation:



where {h,k) = the vertex, a = distance from center to vertex,
and b= distance from vertex to nerest corner of defining 
rectangle.

So (h,k) = (8,0), , 

Therefore the equation is





Edwin