SOLUTION: How do I square the square where needed... x^2+2x+y^2+4y=4

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: How do I square the square where needed... x^2+2x+y^2+4y=4       Log On


   

Question 141518This question is from textbook
: How do I square the square where needed...
x^2+2x+y^2+4y=4
This question is from textbook

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
I think you meant that you want to 'complete the square'

What you are trying to do is develop the equation of a circle in standard form, namely %28x-h%29%5E2%2B%28y-k%29%5E2=r%5E2, an equation of a circle with center at (h,k) and radius r.


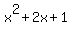So, what do you need to add to x%5E2%2B2x so that you will have a perfect square trinomial? Answer: take the coefficient on the 1st degree term, 2 in this case, divide it by 2, and square the result. You should get 1 if you did the arithmetic correctly. So add 1 to both sides of your original equation. And then the first three terms will be x%5E2%2B2x%2B1 which can be factored to %28x%2B1%29%5E2

Now, perform the same process for the y terms, adding the result to both sides of the original equation, and then factoring the y-terms plus the new constant you added.

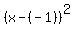Since we know that the first part of the result is %28x%2B1%29%5E2, we know that the x-coordinate of the center of the circle must be -1 (%28x%2B1%29%5E2 is the same as %28x-%28-1%29%29%5E2). Whatever comes up from doing the y-side will give you the other coordinate.

The sum of the original constant term, 4, the 1 you added to complete the square on the x terms, and whatever you added to complete the square of the y terms is the square of the radius.