SOLUTION: Find an equation of a hyperbola with vertices at (-9,4) and (-5,4) and asymptotes y=3x+25 and y=-3x-17.

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find an equation of a hyperbola with vertices at (-9,4) and (-5,4) and asymptotes y=3x+25 and y=-3x-17.       Log On


   

Question 137050: Find an equation of a hyperbola with vertices at (-9,4) and (-5,4) and asymptotes y=3x+25 and y=-3x-17.

Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!
Find an equation of a hyperbola with vertices at (-9,4) and (-5,4) and asymptotes y=3x+25 and y=-3x-17.

First let's draw the asymptotes and the vertices:

We can tell that the hyperbola opens right and left
and has the equation
%28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2=1
where the center is 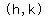%22%28h%2Ck%29%22
The length of the semi-transverse axis is a
The length of the semi-conjugate axis is b
The two asymptotes have slopes ±b%2Fa and pass
through the center (h,k).
The center is the midpoint between the vertices,
(-9,4) and (-5,4) which is the point (-7,4)
So (h,k) = (-7,4)
The transverse axis is the distance between the vertices
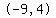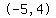%22%28-9%2C4%29%22 and %22%28-5%2C4%29%22 which is 4 units.
So the semi-transverse axis is half of that or 2.
That is a=2
Since the asymptotes are y=3x%2B25 and y=-3x-17
We compare them to y=mx%2BB and find that their slopes
are ±3,
Since the slope are ±b%2Fa, then
b%2Fa=3 and since a=2, we substitute that:
b%2F2=3 or b=6
So the equation
%28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2=1
becomes
%28x-%28-7%29%29%5E2%2F2%5E2%2B%28y-4%29%5E2%2F6%5E2=1
%28x%2B7%29%5E2%2F4%2B%28y-4%29%5E2%2F36=1
Now we draw the defining rectangle which has base
2a and height 2b and has the center as its center.

Now we can sketch in the hyperbola: