Question 124687: The problem is:
Sketch a graph of this equation, find the coordinates of the foci, and find the lengths of the major and minor axes.
3x^2+2y^2=24
I know it may be hard to show how to graph this, so just putting it into the correct form of an ellipse, and then helping me figure out what the foci and axes are would be very helpful! Thanks :)!!
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The problem is:
Sketch a graph of this equation, find the coordinates of the foci,
and find the lengths of the major and minor axes.
3x^2+2y^2=24
I know it may be hard to show how to graph this, so just putting
it into the correct form of an ellipse, and then helping me figure
out what the foci and axes are would be very helpful! Thanks :)!!
We use the fact that the equations of ellipses with centers
at the origin are of two different forms:
 for ellipses which look like this for ellipses which look like this
 ,
and have foci (± ,
and have foci (± ,0) where ,0) where  and
and
 for ellipses which look like this for ellipses which look like this
 and have foci (0,±
and have foci (0,± ) where ) where  You can tell which is which by looking at
the denominators. It is always true that
You can tell which is which by looking at
the denominators. It is always true that
 is larger than is larger than  . .
 represents the semi-major axis, or as some say,
the "long radius" represents the semi-major axis, or as some say,
the "long radius"
 represents the semi-minor axis, or as some say,
the "short radius"
--------
Starting with your equation, represents the semi-minor axis, or as some say,
the "short radius"
--------
Starting with your equation,
 we must get it into one of the forms above. So
we must first get a 1 on the right by dividing
every term through by 24:
we must get it into one of the forms above. So
we must first get a 1 on the right by dividing
every term through by 24:
 which simplifies to
which simplifies to
 Since 12 is larger than 8, we know that
Since 12 is larger than 8, we know that
 and and  and so the
ellipse is of the form and so the
ellipse is of the form
 and looks something
like the second figure above.
Since it has foci (0,± and looks something
like the second figure above.
Since it has foci (0,± ) where ) where  ,
then ,
then
 , ,
 , ,
 , ,

 The foci are
(
The foci are
( ,± ,± )
Now we'll draw the graph, since )
Now we'll draw the graph, since  Then
Then  = =  ,
or about ,
or about  so we draw the major axis
from the vertex point ( so we draw the major axis
from the vertex point (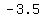 , , ) to the
other vertex point ( ) to the
other vertex point ( , , ) )
 Then we draw the minor axis from (-b,0) to (b,0)
and since
Then we draw the minor axis from (-b,0) to (b,0)
and since  , then , then  , or , or
 , or , or  , or
about , or
about  so we
draw the minor axis from (
so we
draw the minor axis from (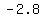 , , ) to
( ) to
( , , ) )
 Now we can sketch in the ellipse and also
indicate the two foci,
(
Now we can sketch in the ellipse and also
indicate the two foci,
( , ± , ± )
with two short lines )
with two short lines
 Edwin
Edwin
|
|
|