Question 1208732: Find the equation of the ellipse with vertex at (0, 0), vertices at (3, 0) and (-3, 0), and eccentricity of 1/3. Identify the parts of the ellipse and sketch the graph.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52799)   (Show Source):
You can put this solution on YOUR website! .
Find the equation of the ellipse with vertex at (0, 0), vertices at (3, 0) and (-3, 0),
and eccentricity of 1/3. Identify the parts of the ellipse and sketch the graph.
~~~~~~~~~~~~~~~~~~~~~
Such an ellipse with three vertices, as described in your post,
does not exist in the nature.
Never existed and can not exist.
This " problem " is a FAKE.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Find the equation of the ellipse with 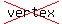 center at (0, 0), vertices at (3, 0) and (-3, 0), and eccentricity of 1/3. Identify the parts of the ellipse and sketch the graph.
The center is at (0,0) and the vertices are at (-3,0) and (3,0), so a, the semi-major axis, is 3.
The eccentricity, e = c/a, is 1/3; with a = 3, c = 1.
For an ellipse, a, b, and c are related by  . With a=3 and c=1, 
b is the semi-minor axis, so the covertices are (0,2sqrt(2)) and (0,-2sqrt(2))
The equation of the ellipse with center (0,0), is 
ANSWERS:
center (0,0)
vertices (-3,0) and (3,0)
covertices (0,2sqrt(2)) and (0,-2sqrt(2))
equation: 
|
|
|
