SOLUTION: Find the equation of the parabola with axis parallel with the x-axis and passing through (4,2), (-4,10) and (-4, -6). Sketch the graph

Click here to see ALL problems on Quadratic-relations-and-conic-sections

Question 1200121: Find the equation of the parabola with axis parallel with the x-axis and passing through (4,2), (-4,10) and (-4, -6). Sketch the graph
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website!
You can start with , but look at the given points, too. Two of them have x coordinate of -4. y value for the symmetry axis is for .
One of the given points is also the vertex, based on this result.

Use each point to make separate equations.

Solve the system for a, b, c.

You might try an online tool, https://www.emathhelp.net/calculators/linear-algebra/gauss-jordan-elimination-calculator/

Answer by ikleyn(52800)   (Show Source):
You can put this solution on YOUR website!
.
Find the equation of the parabola with axis parallel with the x-axis
and passing through (4,2), (-4,10) and (-4, -6). Sketch the graph
~~~~~~~~~~~~~~~~

        This problem is not to make stupid calculations (as other tutor suggests).
        It is to develop your observation skills and mind, as well as the sense of beauty.

Notice that the points (-4,10) and (-4,-6) have the same x-coordinate. Hence, the horizontal axis of the parabola is the perpendicular bisector y= 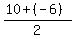= 2 of the segment, connecting (-4,10) and (-4,-6). Also notice that the point (4,2) is the vertex, since it lies on the axis y= 2. So, the vertex form of this parabola is x = a*(y-2)^2 + 4. (*) The coefficient "a" is unknown now. Find it from the condition that the point (-4,10) lies on the parabola. Substitute x=-4, y= 10 into equation (*). You will get -4 = a*(10-2)^2 + 4 -4 - 4 = 64a, ---> 64a = -8 ---> a = = . 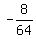So, the equation of the parabola is x = .

Solved.