SOLUTION: Please explain all the steps to my questions 1. The Sum of a number and three times another number is 18. Find the numbers if their product is maximum.

Let one number be x and another number be y.


    +---------------------------------------+
    |    We are given  x + 3y = 18,         |
    |                                       |
    |    so we can express  x = 18 - 3y.    |
    +---------------------------------------+


We are given that the product xy is maximum.


The product xy is

    xy = (18-3y)*y = 18y - 3y^2.


It is a quadratic function of variable y.

Since the coefficient at y^2 is negative  (it is -3), the plot of this quadratic function 
is a downward parabola, which clearly has the maximum.


Its maximum is nothing else as a vertex of the parabola.


To find the position of the maximum point (the position of vertex), there is a general formula for the argument of the quadratic function.


This general formula is 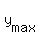  = 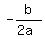,  where "a" is a coefficient at y^2

and b is the coefficient at y of the quadratic function.


In your case, a = -3;  b = 18.  Therefore, the position of the maximum 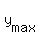 on the coordinate line is

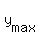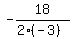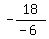     =  =  = 3.


Since we just know y = 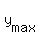 = 3, we can find x = 18 - 3y = 18 - 3*3 = 9.


Thus the answer to the problem is  x= 9;  y= 3.


The problem is just solved.