|
Question 1194678: What is the equation that represents an ellipse with foci at (3, 2) and ( - 9, 2) that passes through the point ( - 3, 10)? Show all steps and provide the answer (the ellipse's equation).
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the equation that represents an ellipse with foci at (3,2) and (-9,2)
that passes through the point (-3,10)? Show all steps and provide the answer
(the ellipse's equation).
~~~~~~~~~~~~~~~~~~~
From the given data, the major axis is horizontal line y = 2.
The center of the ellipse is the point (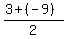 , , ) = (-3,2).
The focal distance between the foci is 3+9 = 12 units;
the eccentricity "c" (half of the focal distance) is c = 12/2 = 6 units.
Since the ellipse passes through the point (-3,10) with the same x-coordinate
as the center has, it implies that the minor semi-axis "b" of the ellipse
has the length of b = 10 - 2 = 8.
Hence, the major semi-axis "a" is a = ) = (-3,2).
The focal distance between the foci is 3+9 = 12 units;
the eccentricity "c" (half of the focal distance) is c = 12/2 = 6 units.
Since the ellipse passes through the point (-3,10) with the same x-coordinate
as the center has, it implies that the minor semi-axis "b" of the ellipse
has the length of b = 10 - 2 = 8.
Hence, the major semi-axis "a" is a = 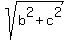 = = 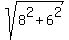 = =  = 10.
Now the equation of the ellipse is = 10.
Now the equation of the ellipse is
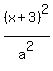 + + 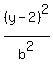 = 1,
or = 1,
or
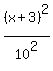 + + 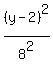 = 1. ANSWER = 1. ANSWER
Solved.
|
|
|
| |