SOLUTION: A satellite follows an elliptical orbit around the earth such that the center of the earth is one of the foci. The farthest point that the satellite will be from the earth’s surf

Since the center of the Earth lies at one focus of the elliptical orbit of the satellite,
we can re-phrase the problem, translating it in this way:


    +------------------------------------------------------------------------------------------+
    | The farthest point of the satellite from the Earth center    is 4000+2500 = 6500 miles   |
    | and the closest point of the satellite from the Earth center is 4000+1000 = 5000 miles.  |
    |                Find the equation of the orbit of the satellite.                          |
    +------------------------------------------------------------------------------------------+


To solve the problem, it is enough to find semi-axes of the elliptical orbit "a" and "b".


For it, use the fact that the greatest distance from the focus to the elliptical orbit
is the sum of the half the focal distance and the major semi-axis "a".


For the closest distance from the focus to the elliptical orbit, it is the difference 
of the major semi-axis "a" and half of the focal distance.


So, if "f" is half of the focal distance between the foci, then we have these two equations

    a + f = 6500  miles   (1)

    a - f = 5000  miles   (2).


By adding equations (1) and (2), you get       2a = 6500+5000 = 11500 miles,  a = 11500/2 = 5750 miles.


By subtracting equations (1) and (2), you get  2f = 6500-5000 =  1500 miles,  f =  1500/2 =  750 miles.


Thus, you just know the parameters "a" and "f" of the ellipce.

Knowing them, you find the minor semi-axis of the ellipse "b" in one line

    b = 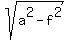 =  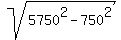= 5700.88 miles (rounded).


Now the standard equation of this ellipse (of this elliptical orbit) is

     +  = 1,

or

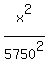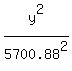     +  = 1.    ANSWER