|
Question 1189357: A parabola having an axis parallel to the y-axis passes through points A(1,1) B(2,2) & C(-1,5). Find the equation
of the parabola.
a. x^2 - 2x - y + 2 = 0
b. y^2 - 2x - y + 2 = 0
c. y^2 - x - 2y + 2 = 0
d. x^2 - x - 2y + 2 = 0
Found 3 solutions by math_tutor2020, greenestamps, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The axis of symmetry is parallel to the vertical y axis means we have a parabola in the form

This parabola either opens upward or opens downward (depending on if a > 0 or a < 0 respectively).
Plug in the coordinates of point A(1,1)




Plug in the coordinates of point B(2,2)




Plug in the coordinates of point C(-1,5)




------------------------------------------------------------
We have this system of equations

which I will refer to as equation (1), equation (2) and equation (3) in that order (from top to bottom).
Let's solve for 'a' in equation (3)


I'll refer to this as equation (4).
Then we'll do the same for equation (1) as well


Let's call this equation (5)
Equations (4) and (5) have 'a' on the left side and something with b's and c's on the right side. Let's equate the right hand sides of those two new equations.

Next, we can add c to both sides



and the c terms cancel.
We can solve for b







------------------------------------------------------------
With this b value in mind, let's go through equations (1), (2) and (3) and plug in b = -2.
Equation 1:




Equation 2:





Equation 3:





We get the exact identical result as before when we plugged b = -2 into equation (1). There's no need to repeat it again, so we ignore this.
The old system we formed earlier was

which is now equivalent to this somewhat reduced system

We've gone from 3 variables + 3 equations down to 2 variables + 2 equations.
------------------------------------------------------------
Solve  for c for c


Plug this into the other equation and solve for 'a'







We can now determine c



------------------------------------------------------------
To recap everything, we have
a = 1
b = -2
c = 2
So the template of

fully updates to


The last step is merely cosmetic in my opinion, but it's to subtract y from both sides to get 0 on its own side by itself.




Answer: Choice A
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The solution from the other tutor is fine... but he went to a lot of trouble to find the equation of the parabola from his original three equations.
y=ax^2+bx+c
(1,1): a+b+c=1 [1]
(2,2): 4a+2b+c=2 [2]
(-1,5): a-b+c=5 [3]
Observe that the coefficients of a and b in [1] and [3] are the same. So subtracting one of those equations from the other will immediately give us b.
2b=-4
b=-2
Now substitute b=-2 in [1] and [2]:
a-2+c=1; a+c=3
4a-4+c=2; 4a+c=6
3a=3
a=1
Substitute a=1 and b=-2 in [1] to find c:
1-2+c=1; c=2
We have a=1, b=-2, c=2.
ANSWER: y=x^2-2x+2 -- which is equivalent to answer choice a
Of course, if this were a question on a multiple choice test, you would simply eliminate answer choices b and c because they contain y^2 terms instead of x^2 terms (making them equations of parabolas with axis parallel to the x-axis). Then you would simply substitute the coordinates of the given points to determine which of answer choices a and d is correct.
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A parabola having an axis parallel to the y-axis passes through points A(1,1) B(2,2) & C(-1,5). Find the equation
of the parabola.
a. x^2 - 2x - y + 2 = 0
b. y^2 - 2x - y + 2 = 0
c. y^2 - x - 2y + 2 = 0
d. x^2 - x - 2y + 2 = 0
~~~~~~~~~~~~~~~
This problem is to restore an equation of a parabola having given three points
that lie on the parabola.
The problems of this kind usually fall in one of two categories.
One category of such problems assumes that you construct the full matrix equation
of 3 equations in 3 unknowns for the coefficients of a quadratic function.
Another category contains some gimmicks that allow to solve a problem in more simple manner.
In the given problem, I see that if I move one unit to the right along x-axis from point A,
I will have the raise of the function of 1 unit.
I also see that if I move two units to the left along x-axis from point A,
I will have the raise of the function of 4 units.
It tells me that the line of symmetry of the parabola is x= 1 through point A and that point A(1,1)
is the vertex of the parabola.
After that, I can write the quadratic function in its vertex form as
y = 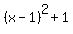 = x^2 - 2x + 2.
It is nothing else as choice (a). = x^2 - 2x + 2.
It is nothing else as choice (a).
Solved (mentally, in my head).
----------------
In the given form, the problem is the kind of " joke Math problems " in this area - - - for those
who does understand Math jokes.
|
|
|
| |