|
Question 1189326: The distance from point A(√6 Cos Ѳ, √2 Sin Ѳ) to the center of the ellipse is equal to 2. If the equation of the ellipse is 2x^2 + 6y^2 = 12, determine the value of Ѳ.
a. 30 b. 60 c. 45 d. 55
Answer by ikleyn(52800)   (Show Source):
You can put this solution on YOUR website! .
The distance from point A(√6 Cos Ѳ, √2 Sin Ѳ) to the center of the ellipse is equal to 2.
If the equation of the ellipse is 2x^2 + 6y^2 = 12, determine the value of Ѳ.
a. 30 b. 60 c. 45 d. 55
~~~~~~~~~~~~~~~~~~
The points with the coordinates of the given form all belong to the ellipse, for any angle  ,
as it is easily can be proven by substituting the coordinates into the ellipse equation.
So, we write equation for the distance
x^2 + y^2 = 2^2,
or
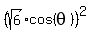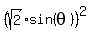 +  = 4,
6*cos^2(theta) + 2*sin^2(theta) = 4
In the last equation, we replace sin^2(theta) by 1-cos^2(theta)
6*cos^2(theta) + 2*(1-cos^2(theta)}}} = 4
4cos^2(theta) = 2
cos^2(theta) = 2/4 = 1/2
cos(theta) = +/-  .
From the last equation, the angle may have any of four values 45°, 135°, 225° or 315°.
The problem does not provide any condition to select from these four opportunities.
If the point is in the first quadrant, then the answer is option (c),
but this assumption is not in the problem.
-------------
In my view, the problem is a typical trap with incomplete input data to catch a student in this trap.
|
|
|
| |
