SOLUTION: A conic has an equation of an asymptote equal to 3x=4y. What is the equation of the conic having its center at origin and its transverse axis equal to y=0. a. 9x2-16y2 = 144 b

Click here to see ALL problems on Quadratic-relations-and-conic-sections

Question 1189325: A conic has an equation of an asymptote equal to 3x=4y. What is the equation of the conic having its center at
origin and its transverse axis equal to y=0.
a. 9x2-16y2 = 144
b. 16x2 - 9y2 = 144
c. 9y2 - 16x2 = 144
d. 16y2 - 9x2 = 144
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200) (Show Source):
You can put this solution on YOUR website!

The transverse axis (connecting the two vertices of the hyperbola) is the line y=0, which is the x-axis, so the branches of the hyperbola open right and left. So the equation is of the form

So we can eliminate choices c and d.

The slopes of the asymptotes are b/a and -b/a. Given that one of the asymptotes has the equation 3x=4y, we have y=(3/4)x; therefore, b/a=3/4. Then the equation is

ANSWER a

Answer by MathLover1(20850) (Show Source):
You can put this solution on YOUR website!

check the first choice:

=> , , ,
=> center (, ) is at origin
The transverse axis is a line segment that passes through the center of the hyperbola and has vertices as its endpoints.
The vertices (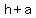, ), (, 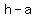) are the two bending points of the hyperbola with center (, ) and semi-axis , .
so,
(, )= (, ) =(,)
(, )=(,)=(,)
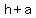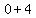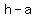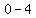so, vertices lie on x-axis, and ->and its transverse axis lies between (,) and (,)

For right-left hyperbola the asymptotes are:
= ±
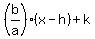
we need only positive

this means, your answer is option a.