|
Question 1189323: Find the tangent line to the parabola x^2 = 6y + 10 through (7,5)
Found 2 solutions by ikleyn, Alan3354:
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the tangent lines to the parabola x^2 = 6y + 10 passing through the point (7,5), which lies outside the parabola.
~~~~~~~~~~~~~~~~
The final equations of the tangent lines are correct in the post by @Alan,
but the logic of his solution is unclear to me.
I tried to understand it, but failed.
Therefore, I developed my own solution in a way as it SHOULD be done:
in a way as my teachers and my textbooks taught me.
An equation of the line passing through the point (7,5) is
y-5 = m*(x-7),
where "m" is the slope coefficient, or
y = mx - 7m +5.
+----------------------------------------------------------------+
| The value of the slope "m" is unknown now, |
| and the rest of the solution is to find the value of "m". |
+-----------------------------------------------------------==---+
Substitute this expression for y into the right side of the parabola formula
x^2 = 6(mx - 7m +5) + 10.
You will get
x^2 - 6mx + 42m - 40 = 0. (1)
The line is tangent to the parabola if and only if the quadratic equation (1) has a unique real root.
It happens if and only if the discriminant of the equation is zero.
The discriminant is d = b^2 - 4ac; b= -6m; a= 1; c= 42m-40, so
d = 36m^2 - 4(42m-40) = 36m^2 - 168m + 160.
Therefore, to find "m", we need solve this quadratic equation
36m^2 - 168m + 160 = 0.
Find its solutions, using the quadratic formula. They are
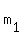 = =  and and  = =  .
So, there are two tangent line through the given point to parabola.
Their equations are y-5 = .
So, there are two tangent line through the given point to parabola.
Their equations are y-5 = 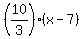 and y-5 = and y-5 = 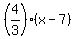 .
The equivalent forms of these equations are
3y - 10x = -55 and 3y - 4x = -13.
The plots are shown in the Figure below. .
The equivalent forms of these equations are
3y - 10x = -55 and 3y - 4x = -13.
The plots are shown in the Figure below.
 Parabola y =
Parabola y = 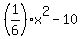 (red) and tangent lines 3y-4x = -13 (green) and 3y-10x = -55 (blue) (red) and tangent lines 3y-4x = -13 (green) and 3y-10x = -55 (blue)
Solved.
-----------------
Notice that I edited the post to make the problem's formulation mathematically clear.
Your original formulation was far from to be perfect.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the tangent line to the parabola x^2 = 6y + 10 through (7,5)
-------
y = (x^2 - 10)/6
y' = x/3 (the slope of lines tangent)
-----
3y = 10x - 55
and
3y = 4x - 13
==============
More later.
---------------
Thru (7,5) ---> y-5 = (x/3)(x - 7)
y-5 = (x^2 - 7x)/3
3y - 15 = x^2 - 7x
y = (x^2 - 7x + 15)/3
y = (x^2 - 10)/6
---
(x^2 - 7x + 15)/3 = (x^2 - 10)/6
2x^2 - 14x + 30 = x^2 - 10
x^2 - 14x + 40 = 0
(x-4)*(x-10) = 0
x = 4, x = 10 --- (ordinates of the tangent points)
x = 4 ---> (4,1)
x = 10 --> (10,15)
----------------
For (4,1) and (7,5):
m = 4/3
y-5 = (4/3)*(x-7)
3y - 15 = 4x - 28
3y = 4x - 13 --- One line
=============
For (10,15) and (7,5):
m = 10/3
y-5 = (10/3)*(x-7)
3y - 15 = 10x - 70
3y = 10x - 55 --- 2nd line
|
|
|
| |