SOLUTION: foci (-2, 3) and (4, 3) b=4 Please help me solve this. Find the general and standard form then graph it. If it is not that much of a hassle, i would also appreciate it so much if

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: foci (-2, 3) and (4, 3) b=4 Please help me solve this. Find the general and standard form then graph it. If it is not that much of a hassle, i would also appreciate it so much if       Log On


   

Question 1187462: foci (-2, 3) and (4, 3) b=4
Please help me solve this. Find the general and standard form then graph it. If it is not that much of a hassle, i would also appreciate it so much if it has a solution. This is all about ellipse. This is the equation that i ended up with %28x-1%29%5E2%2F25%2B%28y-3%29%5E2%2F16=1
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

This is your solution
the equation that in standard form: %28x-1%29%5E2%2F25%2B%28y-3%29%5E2%2F16=1
in general form: x%5E2%2F25+-+%282x%29%2F25+%2B+y%5E2%2F16-%283y%29%2F8+-159%2F400+=+0
graph:





Answer by ikleyn(52802) About Me  (Show Source):
You can put this solution on YOUR website!
.
foci (-2, 3) and (4, 3) b=4
Please help me solve this. Find the general and standard form then graph it.
If it is not that much of a hassle, i would also appreciate it so much if it has a solution.
This is all about ellipse. This is the equation that i ended up with %28x-1%29%5E2%2F25%2B%28y-3%29%5E2%2F16=1
~~~~~~~~~~~~~~~~~~


The method of analysis is close to what I showed you for similar problem under this link

https://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.1187463.html

https://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.1187463.html 



The foci lie on the horizontal line y= 3 --- hence, the major axis of the ellipse is HORIZONTAL.


The center of the ellipse is the point  (1,3) ---  it explains the numbers in the equation of the ellipse.


Further, the distance between the foci is  4 - (-2) = 6 units;  hence, the eccentricity of the ellipse is  c = 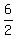6%2F2 = 3 units.


Now you know "c" and "b" of the ellipse:  c = 3, b = 4 (given).  (As a reminder: b is the minor semi-axis).


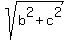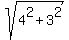You are in position to find the major semi-axis  a = sqrt%28b%5E2+%2B+c%5E2%29 = sqrt%284%5E2%2B3%5E2%29 = sqrt%2825%29 = 5.


After that, the equation of the ellipse is


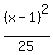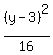    %28x-1%29%5E2%2F25 + %28y-3%29%5E2%2F16 = 1.

Solved, and everything is explained.

---------------

For basic info about ellipses,  see my lesson
    - Ellipse definition, canonical equation, characteristic points and elements
in this site.