Question 1187217: Write the equation of the hyperbola. Co - Ve Vertices: (1, 5) , (1, 1) Focus : (4, 3)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation of the hyperbola:

the length of the transverse axis is 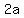
the coordinates of the vertices are ( ± ±  , ,  ) )
the length of the conjugate axis is 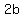
the coordinates of the co-vertices are ( , ,  ± ± ) )
the distance between the foci is 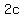 , where , where 
the coordinates of the foci are ( ± ± , ,  ) )
given:
Co -Vertices: ( , ,  ) , ( ) , ( , ,  ) )
we know that the center is half way between: (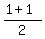 , ,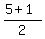 )=( )=( , , ) => so, ) => so,  and and 
use Co -Vertices: ( , ,  ), ),  and and  to find to find 
( , ,  ± ± )=( )=( , ,  ) )
( , ,  ± ± )=( )=( , ,  )=> )=> ± ± =>± =>±
the coordinates of the foci are (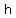 ± ± , ,  )= ( )= ( , , ) =>( ) =>( ± ± , , )= ( )= ( , ,  ) => ) => ± ± =>± =>± =>± =>±
then  => => => =>
and your equation is:


|
|
|