SOLUTION: FIND THE EQUATION OF THE PARABOLA WITH VERTICAL AXIS THAT PASSES THROUGH THE POINT (0,2) AND THE POINTS OF INTERSECTION OF THE PARABOLAS x² + 2x + 3y + 4 = 0 AND x² - 3x+ y + 3 =

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: FIND THE EQUATION OF THE PARABOLA WITH VERTICAL AXIS THAT PASSES THROUGH THE POINT (0,2) AND THE POINTS OF INTERSECTION OF THE PARABOLAS x² + 2x + 3y + 4 = 0 AND x² - 3x+ y + 3 =      Log On


   

Question 1187043: FIND THE EQUATION OF THE PARABOLA WITH VERTICAL AXIS THAT PASSES THROUGH THE POINT (0,2) AND THE POINTS OF INTERSECTION OF THE PARABOLAS x² + 2x + 3y + 4 = 0 AND x² - 3x+ y + 3 = 0.
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
First best to find the intersection points of the two quadratic equations.

system%283y=-x%5E2-2x-4%2Cy=-x%5E2%2B3x-3%29

system%283y=-x%5E2-2x-4%2C3y=-3x%5E2%2B9x-9%29

Equate the expressions for 3y.
system%28-x%5E2-2x-4=-3x%5E2%2B9x-9%29

2x%5E2-11x%2B5=0

discrim, 121-8%2A5=121-40=81=9%5E2
zeros of the quadratic eq.
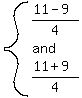
system%28%2811-9%29%2F4%2Cand%2C%2811%2B9%29%2F4%29
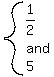system%281%2F2%2Cand%2C5%29----------------(could also have easily been factored if really wanted)

Find the corresponding y values.
y=-3x%5E2%2B3x-3
IF x at 1%2F2, y=-3%2F4%2B3%2F2-3=-3%2F4%2B6%2F4-12%2F4=-9%2F4
IF x at 5, y=-3%2A25%2B15-3=-75%2B15-3=-60-3=-63

The two given parabolas intersect at (1/2, -9/4) and (5, -63).

Now, you want to find equation for the parabola with vertical symmetry axis and containing the three points (0,2), (1/2, -9/4), and (5, -63). You could setup three equations using these points starting in a format ax%5E2%2Bbx%2Bc=y, and solve the system. You continue with that.