Question 1186881: What is the equation of the ellipse having major axis of length 12, center at
(-2,-9), and a focus at (3,-9)?
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Instead of doing yours for you, I'll do one exactly like yours step by step, so
you can use it as a model to do yours by. Here is the problem I will do.
Just use your numbers instead of the ones here:
What is the equation of the ellipse having major axis of length 16, center at
(-3,-8), and a focus at (4,-8)?
 The equation of an ellipse with major axis horizontal is
The equation of an ellipse with major axis horizontal is
     where the center is (h,k) = (-3,-8), and where "a" = semi-major axis length.
The major axis is 16, so the semi-major axis = 8. So far we have
where the center is (h,k) = (-3,-8), and where "a" = semi-major axis length.
The major axis is 16, so the semi-major axis = 8. So far we have
  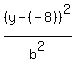  
  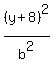   We need "b", which is the semi-minor axis length. We have to use the
Pythagorean theorem relationship for all ellipses, which is
We need "b", which is the semi-minor axis length. We have to use the
Pythagorean theorem relationship for all ellipses, which is
     where c = distance from center to a focus. The distance from the center (-3,-8)
to the focus, which is (4,-8) is 7 units, found by counting units on the graph
above. So b = 7, and the complete equation of the ellipse is
where c = distance from center to a focus. The distance from the center (-3,-8)
to the focus, which is (4,-8) is 7 units, found by counting units on the graph
above. So b = 7, and the complete equation of the ellipse is
  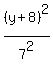  
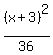  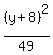   Now do yours exactly, step by step, like this one.
Edwin
Now do yours exactly, step by step, like this one.
Edwin
|
|
|