.
A railroad crosses a highway over an arch a cross section of which is an semi-ellipse 42 meters long
and 12 meters high. there are vertical supports at interval of 7 meters. find the heights and supports.
~~~~~~~~~~~~~~~~~~~~~~~~
An equation of the ellipse is
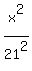 +
+ 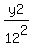 = 1.
From equation, express
y =
= 1.
From equation, express
y = 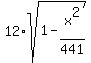 .
The supports are at x = -14, -7, 0, 7, 14.
Therefore, what you need is to calculate this sum
Sum =
.
The supports are at x = -14, -7, 0, 7, 14.
Therefore, what you need is to calculate this sum
Sum = 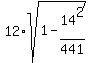 +
+ 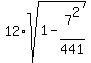 +
+ 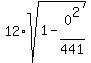 +
+ 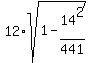 +
+ 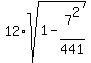 .
The sum is 52.52 meters (rounded). ANSWER
.
The sum is 52.52 meters (rounded). ANSWER
Solved.