Question 1186658: An ellipse has vertices (2 − √ 61, 5) and (2 + √ 61, 5), and its minor axis is 12 units long. Find its standard equation and its foci.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
An ellipse has vertices (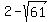 , ,  ) and ( ) and (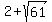 , ,  ), and its minor axis is ), and its minor axis is  units long. units long.
Find its standard equation and its foci.
center is half way between vertices
(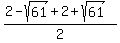 , ,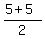 )=( )=( , , )=( )=( , , )=> )=> and and 
minor axis is  => =>
 ........plug in known ........plug in known

 ...............plug in coordinates of vertices ( ...............plug in coordinates of vertices (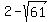 , ,  ) )




so, your equation is:

for an ellipse with major axis parallel to the x-axis, the Foci (focus ) are defined as :
(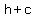 , ,  ), ( ), (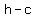 , ,  ) )
find 



 or or 
(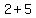 , , )=( )=( , ,  ) )
( , , ) =( ) =( , , ) )

Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An ellipse has vertices (2 − √ 61, 5) and (2 + √ 61, 5), and its minor axis is 12 units long.
Find its standard equation and its foci.
~~~~~~~~~~~~~~
It can be done (and it should be done) in much shorter way, than @MathLover1 does it.
It does not require so intensive calculations.
Looking at the foci coordinates, you see that they are on the horizontal line y = 5.
So, the major axis is horizontal, parallel to x-axis, and the length of the horizontal axis is
 - - 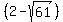 = = 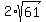 .
Hence, the length of the major semi-axis "a" is half of it, i.e. a = .
Hence, the length of the major semi-axis "a" is half of it, i.e. a =  .
The length of the minor semi-axis is b = .
The length of the minor semi-axis is b =  = 6.
The center of the ellipse is the point (2,5).
THEREFORE, the standard form equation of the ellipse is = 6.
The center of the ellipse is the point (2,5).
THEREFORE, the standard form equation of the ellipse is
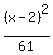 + + 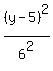 = 1. ANSWER
The distance from the center to the focus is c = = 1. ANSWER
The distance from the center to the focus is c = 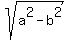 = = 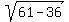 = =  = 5.
The foci are (2+5,5) = (7,5) and (2-5,5) = (-3,5). = 5.
The foci are (2+5,5) = (7,5) and (2-5,5) = (-3,5).
Solved.
|
|
|