Question 1186254: Vertices: (15, 1), (-1, 1); Endpoints of Conjugate Axis: (7, 7),
(7, -5)
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Vertices: ( , ,  ), ( ), ( , ,  ); );
Endpoints of Conjugate Axis: ( , ,  ), ( ), ( , ,  ) )
-> the center is at midpoint (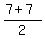 , , 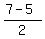 )=> C ( )=> C ( , ,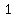 ) )
the length of Conjugate Axis is  => =>
equation of hyperbola
 ........plug in known ........plug in known

 ........use vertices ( ........use vertices ( , ,  ) to calculate ) to calculate 




so, your equation is:


Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Vertices: (15, 1), (-1, 1); Endpoints of Conjugate Axis: (7, 7), (7, -5).
~~~~~~~~~~~~~~~~~~~
Since the conjugate axis is mentioned, it is about hyperbola.
Its center is the point (7,1).
It has horizontal major axis y = 1, parallel to x-axis.
The distance between vertices is 15 - (-1) = 16; hence, the major semi-axis length "a" is 16/2 = 8 units.
It has vertical conjugate axis x = 7, parallel to y-axis.
The length of the conjugate axis is 7 - (-5) = 12; hence, the minor semi-axis length "b" is 12/2 = 6 units.
Combining all this info, the standard equation of the hyperbola is
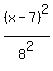 - - 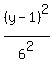 = 1. = 1.
Solved.
|
|
|