Question 1185877: Write the equation of the ellipse with its vertex at the origin, length of the major axis 10, foci on x-axis, ellipse passes through the point (√5,2)
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(Edited response.... I am not accustomed to the use of the term vertex when talking about ellipses, so I assumed the problem was supposed to have the center of the ellipse at the origin. Doing that also results in a simpler equation for the ellipse, so possibly it was the intent of the problem that the origin is the center of the ellipse. If that is not the case, then see the solution by tutor @ikleyn.)
CENTER at the origin -- not the "vertex"
General equations:
(1) major axis horizontal: 
(2) major axis vertical: 
(h,k) is the center
a is length of semi-major axis
b is length of semi-minor axis
In this example....
center is at the origin, so h=k=0
major axis is 10 so a=5
foci are on the x-axis, so major axis is horizontal
That gives us, for the equation so far....

Complete the equation by finding the value of b^2, using the given point on the ellipse, (x,y)=(sqrt(5),2).




ANSWER: 
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write the equation of the ellipse with its vertex at the origin, length of the major axis 10,
foci on x-axis, ellipse passes through the point (√5,2)
~~~~~~~~~~~~~~~~~~~~~~~
In his post, tutor @greenestamps changed the problem and presented the solution for different problem.
Here, in this post, I will give a solution to the problem "as it is" without any changes in it.
The length of the major axis is 10 units - hence, the major semi-axis is 5 units long.
Foci are on x- axis - hence, the major axis is x-axis (horizontal), and the ellipse is
more long horizontally than wide vertically.
The point on the ellipse is (√5,2). It tells that the ellipse in entirely in the positive
half-plane x >= 0. In particular, his center is at (5,0).
So, the equation of the ellipse is
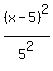 + +  = 1.
To find "b", use the coordinates of the point ( = 1.
To find "b", use the coordinates of the point ( , , ), substituting them into this equation ), substituting them into this equation
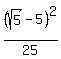 + + 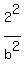 = 1.
Simplify = 1.
Simplify
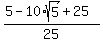 + +  = 1, = 1,
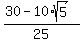 + +  = 1, = 1,
 = 1 - = 1 - 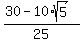 , ,
 = = 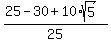 = = 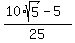 = = 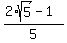 .
So, b^2 = .
So, b^2 = 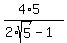 = = 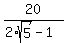 .
Therefore, the ellipse equation is .
Therefore, the ellipse equation is
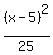 + + 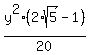 = 1. = 1.
Solved.
|
|
|