SOLUTION: A parabolic searchlight is 5ft across its opening. If the light source is located 2ft from the base along the axis of symmetry, how deep (in feet) should be the searchlight?

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: A parabolic searchlight is 5ft across its opening. If the light source is located 2ft from the base along the axis of symmetry, how deep (in feet) should be the searchlight?      Log On


   

Question 1185766: A parabolic searchlight is 5ft across its opening. If the light source is located 2ft from the base along the axis of symmetry, how deep (in feet) should be the searchlight?
Answer by ikleyn(52798) About Me  (Show Source):
You can put this solution on YOUR website!
.
A parabolic searchlight is 5ft across its opening. If the light source is located 2ft from the base
along the axis of symmetry, how deep (in feet) is the searchlight?
~~~~~~~~~~~~~~~~~~~ 


The diameter of the searchlight is 5 ft at the opening.


From the general theory, if the focal distanse (the distance from the parabola vertex to the focus of the parabola) is p units,

then the equation of the parabola is  y = 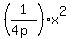%281%2F%284p%29%29%2Ax%5E2.


In our case, the focal distance is 2 feet (given), i.e.  p = 2.


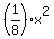HENSE, the parabola equation is  y = %281%2F%284%2A2%29%29%2Ax%5E2,  or  y = %281%2F8%29%2Ax%5E2.



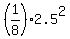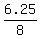THEREFORE, at x= 2.5 ft (radius of the opening, given),  y = %281%2F8%29%2A2.5%5E2 = 6.25%2F8 = 0.78125 ft.


ANSWER.  The searchlight is 0.78125 ft deep.

Solved.