|
Question 1185514: A satellite dish in the shape of a paraboloid is 10 ft across, and 4 ft deep at its vertex. How far is the receiver from the vertex, if it is placed at the focus? Round off your answer to 2 decimal places.
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A satellite dish in the shape of a paraboloid is 10 ft across,
and 4 ft deep at its vertex. How far is the receiver from the vertex,
if it is placed at the focus? Round off your answer to 2 decimal places.
~~~~~~~~~~~~~~~~~~
In plane section of the paraboloid, we have a parabola.
We consider this parabola as opened upward with the vertex at the origin of the coordinate system.
About this parabola, we know that the y-value is 4 ft, when the x-value is 5 ft.
We want to restore the parabola equation, so we write
y =  . (1)
To find the coefficient "a", we substitute y= 4 and x= 5 into this equation. We get then
4 = . (1)
To find the coefficient "a", we substitute y= 4 and x= 5 into this equation. We get then
4 = 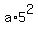 , or a = , or a = 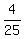 ,
so the equation (1) of the parabola takes the form
y = ,
so the equation (1) of the parabola takes the form
y = 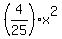 . (2)
+----------------------------------------------------------------------------------+
| Half of the problem is just solved. |
| |
| Now we should find the focal distance of the parabola, given by equation (2). |
+----------------------------------------------------------------------------------+
Generally, if the parabola has equation y = . (2)
+----------------------------------------------------------------------------------+
| Half of the problem is just solved. |
| |
| Now we should find the focal distance of the parabola, given by equation (2). |
+----------------------------------------------------------------------------------+
Generally, if the parabola has equation y = 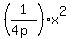 , then the focal distance is p.
So, we should write equation (2) in this form. For it, we write
y = , then the focal distance is p.
So, we should write equation (2) in this form. For it, we write
y = 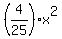 = = 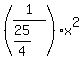 = = 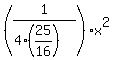 ,
and we see that the parameter p is equal to p = ,
and we see that the parameter p is equal to p =  = 1.5625 ft = 1.56 ft (rounded to two decimal places).
ANSWER. The receiver should be 1.56 ft from the vertex (the precise distance is 1.5625 ft). = 1.5625 ft = 1.56 ft (rounded to two decimal places).
ANSWER. The receiver should be 1.56 ft from the vertex (the precise distance is 1.5625 ft).
Solved.
|
|
|
| |