SOLUTION: Can you help me with these? Please Find the standard form of the equation of the hyperbola with; 1. F_1 (5,0), F_2 (-5,0) V_1 (4,0), V

Click here to see ALL problems on Quadratic-relations-and-conic-sections

Question 1185036: Can you help me with these? Please
Find the standard form of the equation of the hyperbola with;
1. F_1 (5,0), F_2 (-5,0)
V_1 (4,0), V_2 (-4,0)
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850) (Show Source):
You can put this solution on YOUR website!
the standard form of the equation of the hyperbola with;
1.
(,), (,)
(,)=>
(,), (,)
(,) =>

=>
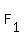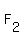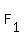=> Co-vertices: (,), (,)
=> center is at origin
Major (transverse) axis length: distance between vertices
Semi-major axis length:
Minor (conjugate) axis length:
Semi-minor axis length:
equation of the hyperbola:

Answer by Edwin McCravy(20059) (Show Source):
You can put this solution on YOUR website!

We plot those given points and sketch in a rough sketch of the hyperbola. All "conic" graphs curve around their focal points. The equation of all hyperbolas that open right and left have equations, where (h,k) is the center, "a" is the distance between the center and either vertex. "c" is the distance between the center and either focal point (or focus). But "c" does not appear in the standard equation of a hyperbola. We calculate "b²" by the Pythagorean theorem: The center is (0,0), so h=0, k=0, a²=4^2=16, b²=3^2=9. Substitute in Edwin

SOLUTION: Can you help me with these? Please Find the standard form of the equation of the hyperbola with; 1. F_1 (5,0), F_2 (-5,0) V_1 (4,0), V_2 (-4,0)