|
Question 1184727: Suppose that the orbit of a planet is in the shape of an ellipse with major axis
whose length is 500 million km. If the distance between the foci is 400 million
km, find an equation of the orbit.
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose that the orbit of a planet is in the shape of an ellipse with major axis
whose length is 500 million km.
If the distance between the foci is 400 million km, find an equation of the orbit.
~~~~~~~~~~~~~~~~~
To write the ellipse's equation, we should know the lengths of the two semi-axes.
For the major semi-axis "a", we just know it: it is half of 500 million km, or a = 250 millions of km.
We also know the half of the distance between the foci, which is c = 400/2 = 200 millions of kilometers.
Third thing which we know is this relation between "a", "b" and "c"  = =  - -  ,
where "b" is the minor semi-axis. It gives us ,
where "b" is the minor semi-axis. It gives us
 = =  - -  = =  - - 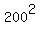 = = 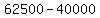 = = 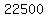 = = 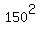 millions km^2.
THEREFORE, the equation of the ellipse is millions km^2.
THEREFORE, the equation of the ellipse is
 + + 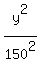 = 1,
where x and y are the coordinates of the planet (of the center of the planet) on the orbit, in millions of kilometers. = 1,
where x and y are the coordinates of the planet (of the center of the planet) on the orbit, in millions of kilometers.
Solved and explained.
--------------------------
For the ellipse canonical equation, see the first lesson from this list
- Ellipse definition, canonical equation, characteristic points and elements
- Ellipse focal property
- Tangent lines and normal vectors to a circle
- Tangent lines and normal vectors to an ellipse
- Optical property of an ellipse
- Optical property of an ellipse revisited
in this site.
For the properties of ellipses, read from the rest of the lessons, and find there many interesting issues,
which you, probably, will not find in other sources.
|
|
|
| |