|
Question 1184285: If two circles  and and  intersect orthogonally, then what is the value of k? intersect orthogonally, then what is the value of k?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If two circles  and and  intersect orthogonally, then what is the value of k? intersect orthogonally, then what is the value of k?
~~~~~~~~~~~~~~~~
As posed, this problem HAS NO SOLUTION,
and I will show it RIGHT NOW.
First circle

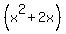 + + 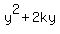 = -6 = -6
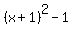 + + 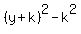 = -6 = -6
 + + 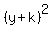 = - 6 + 1 + k^2 = - 6 + 1 + k^2
 + + 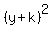 = k^2 - 5
has the center at the point (-1,-k) and the radius of = k^2 - 5
has the center at the point (-1,-k) and the radius of 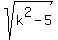 .
Note that the condition k^2 >= 5 is the NECESSARY condition for existing such a circle.
Second circle .
Note that the condition k^2 >= 5 is the NECESSARY condition for existing such a circle.
Second circle

 + + 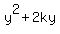 = -k = -k
 + + 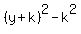 = -k = -k
 + + 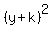 = k^2-k
has the center at the point (0,-k) and the radius of = k^2-k
has the center at the point (0,-k) and the radius of 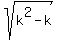 .
Note that the condition k^2 - k >= 0 is the NECESSARY condition for existing such a circle.
The line connecting the centers is horizontal y = -k, and the distance between the centers is 1 unit.
So, we have a right angled triangle, formed by the line of centers as the hypotenuse of 1 unit long,
and the legs, that are the radii, drawn to the intersection point, of the lengths found above.
Next, we write the Pythagorean equation .
Note that the condition k^2 - k >= 0 is the NECESSARY condition for existing such a circle.
The line connecting the centers is horizontal y = -k, and the distance between the centers is 1 unit.
So, we have a right angled triangle, formed by the line of centers as the hypotenuse of 1 unit long,
and the legs, that are the radii, drawn to the intersection point, of the lengths found above.
Next, we write the Pythagorean equation
 + + 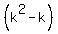 = 1,
which gives
2k^2 - k - 6 = 0.
From this equation, the roots are = 1,
which gives
2k^2 - k - 6 = 0.
From this equation, the roots are
 = = 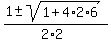 = = 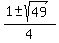 .
Thus the two possible roots are k= 2 and k= -1.5.
But no one of these values of k satisfies the necessary condition k^2 >= 5.
THEREFORE, the problem, as it is posed, HAS NO SOLUTION. .
Thus the two possible roots are k= 2 and k= -1.5.
But no one of these values of k satisfies the necessary condition k^2 >= 5.
THEREFORE, the problem, as it is posed, HAS NO SOLUTION.
Solved (or better to say, DISPROVED).
----------------
For your safety, IGNORE the post by @MathLover1, since her answer is WRONG.
|
|
|
| |