|
Question 1183865: Find the equation of the locus of a point which moves so that its distance from the point (1,-1) is three times its distance from the line y = 3.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the equation of the locus of a point which moves so that its distance
from the point (1,-1) is three times its distance from the line y = 3.
~~~~~~~~~~~~~~~
The setup equation is INCORRECT in the post by @josgaritmetic.
THEREFORE, his "solution" is WRONG from the very first line to very last line.
For your safety, ignore his post.
I came to bring a correct solution.
Write the equation for distances, as you read the problem
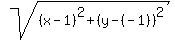 = 3*|y-3|,
or = 3*|y-3|,
or
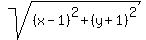 = 3*|y-3|.
Square both sides
(x-1)^2 + (y+1)^2 = 9*(y-3)^2.
Simplify and reduce to the standard conic section equation
(x-1)^2 + y^2 + 2y + 1 = 9y^2 - 54y + 81
(x-1)^2 - 8y^2 + 56y + 1 = 81
(x-1)^2 - 8(y^2 - 7y) + 1 = 81
(x-1)^2 - 8(y^2 - 2*3.5y + 3.5^2) + 8*3.5^2 + 1 = 81
(x-1)^2 - 8(y-3.5)^2 = 81 - 8*3.5^2 - 1
(x-1)^2 - 8(y-3.5)^2 = - 18
8(y-3.5)^2 - (x-1)^2 = 18 = 3*|y-3|.
Square both sides
(x-1)^2 + (y+1)^2 = 9*(y-3)^2.
Simplify and reduce to the standard conic section equation
(x-1)^2 + y^2 + 2y + 1 = 9y^2 - 54y + 81
(x-1)^2 - 8y^2 + 56y + 1 = 81
(x-1)^2 - 8(y^2 - 7y) + 1 = 81
(x-1)^2 - 8(y^2 - 2*3.5y + 3.5^2) + 8*3.5^2 + 1 = 81
(x-1)^2 - 8(y-3.5)^2 = 81 - 8*3.5^2 - 1
(x-1)^2 - 8(y-3.5)^2 = - 18
8(y-3.5)^2 - (x-1)^2 = 18
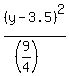 - - 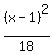 = 1.
The last equation describes a hyperbola with the center at the point (1,3.5),
vertical real semi-axis of the length = 1.
The last equation describes a hyperbola with the center at the point (1,3.5),
vertical real semi-axis of the length 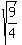 = =  (tranverse semi-axis),
and horizontal imaginary semi-axis of the length (tranverse semi-axis),
and horizontal imaginary semi-axis of the length 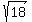 = = 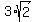 .
The hyperbola is open vertically up and down. .
The hyperbola is open vertically up and down.
Solved.
----------------
For hyperbola, its canonical equation, standard form equation, general equation, elements and properties,
see the lessons
- Hyperbola definition, canonical equation, characteristic points and elements
- Hyperbola focal property
- Tangent lines and normal vectors to a hyperbola
- Optical property of a hyperbola
- Standard equation of a hyperbola
- Identify elements of hyperbola given by its standard equation
- Find the standard equation of a hyperbola given by its elements
- General equation of a hyperbola
- Transform general equation of a hyperbola to the standard form by completing the square
- Identify elements of a hyperbola given by its general equation
- OVERVIEW of lessons on hyperbolas
Also, you have this free of charge online textbook in ALGEBRA-II in this site
ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Conic sections: Hyperbolas. Definition, major elements and properties. Solved problems".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
/////////////
After seeing my post, @josgarithmetic rewrote his setup exactly as my, so now his post is safe (although useless).
At least, I forced him to make it safe . . .
|
|
|
| |