|
Question 1183792: Locate the vertex, the focus, and the ends of the latus rectum and find the equation of the directrix, then draw the parabola whose equation is (y-1)² = -8(x-2).
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Locate the vertex, the focus, and the ends of the latus rectum and find the equation of the directrix, then draw the parabola whose equation is

vertex form

=> , ,  , ,  => => 
vertex at ( , ,  )= ( )= ( , ,  ) )
and focal length: 
parabola is symmetric around the x-axis and so the directrix is a line parallel to the y-axis, a distance: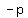 from the center ( from the center ( , ,  ) x-coordinate ) x-coordinate
so, directrix is a line
=>
the latus rectum is the distance between the 2 points on the parabola that are on vertical line that goes through the focus.
the focus is at ( , ,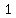 ), and vertical line that goes through the focus y-axis or ), and vertical line that goes through the focus y-axis or 



 or or 
the ends of the latus rectum:( , , ), ( ), ( , , ) )
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
From
(y-1)² = -8(x-2)
the -2 tells that the x-coordinate of the vertex is +2.
the -1 tells that the y-coordinate of the vertex is +1.
So the vertex is (1,2)
The fact that the sign before the 8 is negative tells us that the parabola
opens leftward.
The fact that the x is in the expression that is not squared tells
us the that its axis of symmetry is horizontal, and opens right or left.
The absolute value of the -8, or 8, tells us two things.
1. 8 divided by 4, which is 2, is the distance between the vertex and the
focus (2 is also the perpendicular distance from the vertex to the
directrix).
So the focus is 2 units from the vertex, inside the parabola.
So the focus is (0,1)
And the dirctrix is a vertical line 2 units from the vertex outside the
parabola, so it is the vertical line whose equation is y = 4.
2. The latus rectum (vertical distance across the parabola at the focus) is 8 units long.
The ends of the latus rectum is 4 units up and down from the focus, which
are (0,5) and (0,-3)
 Edwin
Edwin
|
|
|
| |