SOLUTION: Locate the center, vertices, the foci, and the ends of the latera recta then graph the ellipse whose equation is 4x²+9y²-16x+18y-11=0.

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Locate the center, vertices, the foci, and the ends of the latera recta then graph the ellipse whose equation is 4x²+9y²-16x+18y-11=0.      Log On


   

Question 1183607: Locate the center, vertices, the foci, and the ends of the latera recta then graph the ellipse whose equation is 4x²+9y²-16x+18y-11=0.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
4x%5E2%2B9y%5E2-16x%2B18y-11=0
4%28x%5E2-4x%29%2B9%28y%5E2%2B2y%29=11
4%28x%5E2-4x%2B4%29%2B9%28y%5E2%2B2y%2B1%29=11%2B4%2A4%2B9%2A1
4%28x-2%29%5E2%2B9%28y%2B1%29%5E2=11%2B16%2B9
4%28x-2%29%5E2%2B9%28y%2B1%29%5E2=36
The equation above shows that that system%28x-2=0%2Cy%2B1=0%29 or system%28x=2%2Cy=-1%29 are axes (of symmetry) of the ellipse.
The center of the ellipse is the point where they intersect:
the point P%282%2C-1%29
Your teacher may like to write the equation as %28x-2%29%5E2%2F9%2B%28y%2B1%29%5E2%2F4=1 or %28x-2%29%5E2%2F3%5E2%2B%28y%2B1%29%5E2%2F2%5E2=1 ,
dividing by 36 both sides of
4%28x-2%29%5E2%2B9%28y%2B1%29%5E2=36 .
They are just equivalent equations for the same ellipse.
You could say they show more clearly that for all the points of the ellipse
%28x-2%29%5E2%2F9%3C=1 --> abs%28x-2%29%3C=3 and %28y%2B1%29%5E2%2F4%3C=1 --> abs%28y%2B1%29%3C=2
They also show that the vertices of the ellipse are on the axes at system%28y=-1%2Cx=2+%2B-+3%29 and system%28x=2%2Cy=-1+%2B-+2%29
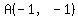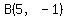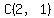at A%28-1%2C-1%29 , B%285%2C-1%29 , C%282%2C1%29 , and D%282%2C-3%29 .
The segment AB, on the "horizontal" y=-1 axis, is called the major axis, because for this ellipse it is longer, going a=3 units to left and right of the center of the ellipse.
The segment CD, on the "vertical" x=2 axis, is called the minor axis, because for this ellipse it is shorter, going b=2 units up and down from the center of the ellipse.
The foci are on the major axis at a distance c to both sides of the center, and we calculate c from a%5E2=b%5E2%2Bc%5E2 .
c=sqrt%283%5E2-2%5E2%29=sqrt%289-4%29=sqrt%285%29 .
Soo the coordinates of the foci are system%28y=-1%2C+x=2+%2B-sqrt%285%29%29 .
The ends of the latera recta are the points on the ellipse with the same 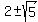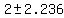x%22=%222+%2B-sqrt%285%29%22=%22approximately2%2B-+2.236 as the foci.
For those points x-2=%22+%22+%2B-sqrt%285%29 , so %28x-2%29%5E2=5
The y coordinates for those points can be calculated from 4%28x-2%29%5E2%2B9%28y%2B1%29%5E2=36 as
4%2A5%2B9%28y%2B1%29%5E2=36-->20%2B9%28y%2B1%29%5E2=36-->9%28y%2B1%29%5E2=16-->%28y%2B1%29%5E2=16%2F9-->y%2B1=%22+%22+%2B-sqrt%2816%2F9%29-->y=-1+%2B-+4%2F3