MathLover1 is absolutely right! I was doing
some copy and pasting, and invertently
copied and pasted an exponent of 2 where it
should not have been. I was lucky that the
squaring was only of the number 1. Here is
the entire solution corrected:
------------------------------------------------------------------
The axis of symmetry is the line through the vertex and the focus, which is
the line through (5, -3) and (6, -3) is y = -3, the yellowish green line.
Since the axis of symmetry is horizontal, the equation is of the form
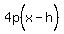where (h,k) is the vertex.
So far we have (h,k) = (5,-3)
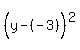
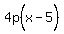
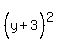
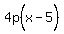The directrix, which is always outside the parabola, is always such that the
perpendicular distance from the vertex to it is the same as the distance
between the vertex and the focus, this distance is |p|, and the sign of p
I taken positive if the parabola opens up or right and negative if the
parabola opens down or left. This one opens right.
Since the vertex and focus are 1 unit apart, the directrix is the vertical
line x = 4, the bright green line, and p=+1 so the equation is
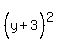
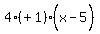
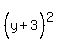
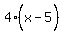I'm not familiar with the notation E1 and E2. I'm guessing that E1 and E2
are the ends of the latus rectum, or focal chord, the vertical line segment
that goes through the focus, the blue line segment. Its length is the same
as 4p.
So we plug x = 6 in the equation and solve for y:
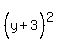
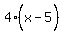
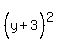
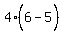
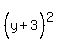
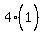
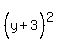
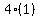
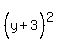
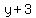
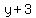
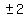Using the "+", y+3 = 2, y = -1, so E1 = (6,-1)
Using the "-", y+3 = -2, y = -5, so E2 = (6,-5)
We find that its length is 4, which is the same as 4p.
If I guessed wrong about E1 and E2, tell me how your
book or teacher defines them in the thank-you note
at the bottom of this page and I'll get back to you
by email.
Edwin
