Question 1181020: Dear Sir/Ma'am
Please Help me solve this problem.
Find the equation if the Ellipse with center at (2,3), Vertices at (2,9) and (2,-3) and Eccentricity of 2/3/ Identify the parts of the Ellipse and sketch the graph.
Parts of the Ellipse
1. Center
2. Foci
3. Vertices V1, V2
4. Co Vertices B1, B2
5. Endpoints of Latus Rectum E1, E2, E3, E4
6. Directrices
7. Eccentricity
8. Length of LR
9. Length of Major Axis
10. Length of Minor Axis
Thank you and GOD Bless
Sincerely Yours,
Lorna
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! equation:

given:
center at ( , , )=> )=> and and 
Vertices at ( , , ) and ( ) and ( , , ) )
as you can see major axis is parallel to y-axis, so it is  ,the ellipse is vertical ,the ellipse is vertical
and distance between vertices is 
=>
so far your equation is:

given ccentricity of 
The eccentricity (e) of an ellipse is the ratio of the distance from the center to the foci (c) and the distance from the center to the vertices (b).




now find minor axis 



semimajor axis length : 
semiminor axis length:  ≈ ≈
major axis length : 
minor axis length: 
foci:
( , , 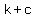 ), ( ), ( , ,  ) )
=>( , , 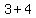 ), ( ), ( , , 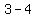 ) )
=>( , ,  ), ( ), ( , ,  ) )
foci:
( , ,  ) , ( ) , ( , , 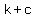 ) )
( , , 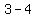 ) , ( ) , ( , , 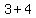 ) )
( , ,  ) , ( ) , ( , ,  ) )
covertices:
( , ,  ) ,( ) ,(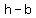 , ,  ) )
(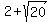 , ,  ), ( ), (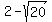 , ,  ) )
≈( , ,  ) , ( ) , (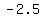 , ,  ) )
eccentricity: 
directrices: since you have vertical ellipse, directrices are  from each y coordinate of the vertices from each y coordinate of the vertices


First directrix: 
Second directrix: 
Endpoints of Latus Rectum
The chord of the ellipse through its one focus and perpendicular to the major axis (or parallel to the directrix) is called the latus rectum of the ellipse.
since foci is at: ( , ,  ) , ( ) , ( , ,  ) )
first latus rectum: 
substitute in ellipse formula and you get
 or or 
two Endpoints of Latus Rectum are
E1= , , and E1= and E1=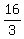 , ,
second latus rectum: 
 same as above same as above
E3= , , and E4= and E4=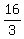 , ,

|
|
|