|
Question 117294: write the equation of the ellipse in standard form having the given properties.
center(4,6) vertex(9,6)(0,8) is on the ellipse
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! write the equation of the ellipse in standard form having the given properties.
center(4,6) vertex(9,6)(0,8) is on the ellipse
Plot those points
 Sketch in the ellipse approximately:
Sketch in the ellipse approximately:
 Since the ellipse is wider than it is tall, it has the
standard equation
Since the ellipse is wider than it is tall, it has the
standard equation
 = 1
And since the center is (h,k) = (4,6), we have = 1
And since the center is (h,k) = (4,6), we have
 = 1
Now we draw in the semi-major axis, which connects the
center to the vertex: = 1
Now we draw in the semi-major axis, which connects the
center to the vertex:
 We can observe that the semi-major axis is 5 units long, so
we know that a = 5, so we can substitute that and our
equation so far is:
We can observe that the semi-major axis is 5 units long, so
we know that a = 5, so we can substitute that and our
equation so far is:
 = 1
or = 1
or
 = 1
Now since we know that the ellipse contains the point
(x,y) = (0,8), we substitute = 1
Now since we know that the ellipse contains the point
(x,y) = (0,8), we substitute
 = 1 = 1
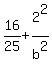 = 1 = 1
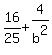 = 1
Clear of fractions by multiplying through by LCD = = 1
Clear of fractions by multiplying through by LCD = 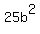



 Since b is the length of the semi-minor axis,
we can now draw in the semi-minor axis 10/3 or
3
Since b is the length of the semi-minor axis,
we can now draw in the semi-minor axis 10/3 or
3 units long, which goes from the
center up to the ellipse: units long, which goes from the
center up to the ellipse:
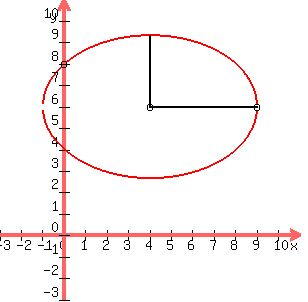 To draw the ellipse more accurately we can now sketch
in the complete major and minor axes:
To draw the ellipse more accurately we can now sketch
in the complete major and minor axes:
 To finish the equation, we substitute
To finish the equation, we substitute 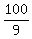 for for 
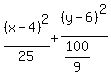 = 1
and that is the desired equation in standard form.
Edwin = 1
and that is the desired equation in standard form.
Edwin
|
|
|
| |