Question 1168920: Find the equation of the ellipse if the endpoints of minor axis are (1,3) and (1,-1) with a focus at (-1,1).Express your answer in general form.
Answer by MathLover1(20853)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The equation of an ellipse can be given as,

where
' ' represents the semi-major axis (half of the length of the major axis) ' represents the semi-major axis (half of the length of the major axis)
' ' represents the semi-minor axis (half of the length of the minor axis) ' represents the semi-minor axis (half of the length of the minor axis)
‘ ’ represents the ’ represents the 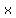 coordinate of the center coordinate of the center
‘ ’ represents the ’ represents the  coordinate of the center coordinate of the center
if the endpoints of minor axis are ( , , ) and ( ) and ( , , ) , minor axis length is equal to the distance between them which is ) , minor axis length is equal to the distance between them which is 
half of the length of the minor axis is 
=> the center mast be half way between endpoints, and it is at ( , , ) )
a focus at ( , , ) )
the distance between foci ( , , ) and center ( ) and center ( , , ) )
focus is  units from the center, so units from the center, so 
using the Pythagorean fact of all ellipses


so, your formula is


|
|
|