Question 1158928: Write the equation of each ellipse or hyperbola.
13. A vertical ellipse has a focus (−6,1). It has a co-vertex of (-10, -7)
The correct answer is:

However, I do not know how to do the work to get the answer
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A vertical ellipse has a focus ( , , ). It has a co-vertex of ( ). It has a co-vertex of ( , ,  ) )
formula for ellipse a 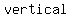 is: is:

co-vertex (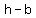 , , ) and ( ) and ( , , ) )
if one co-vertex of ( , ,  ), then => ), then =>
 , , 
focus is at ( , ,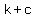 ) and ( ) and ( , , ) )
if one focus ( , , ) , then ) , then
 , ,
 , ->since , ->since 


the other one focus is at
( , ,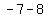 )=( )=( , , ) )
The center is half way between, at ( , ,  ) )
since
 and and  => =>  => => -> ->

other co-vertex is at ( , , )=( )=(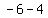 , , )=( )=( , , ) )
find 




and your equation is:

|
|
|