|
Question 1158015: What is the standard and general equation of a parabola with vertex as (-1,2) and directrix of x=-3?
Found 2 solutions by josgarithmetic, MathLover1:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! This means that focus is point (2,2). The parabola is points (x,y) equally distant from both the point (2,2) and the line x=-3.
.
If you start with Distance Formula definition for parabola, you have

Algebra steps will be able to lead to  . .
.
.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
What is the standard and general equation of a parabola with vertex as ( , , ) and directrix of ) and directrix of  ? ?
recall:
The standard form is  , where the focus is ( , where the focus is ( , , 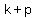 ) and the directrix is ) and the directrix is  . .
If the parabola is rotated so that its vertex is ( , , ) and its axis of symmetry is parallel to the x-axis, it has an equation of ) and its axis of symmetry is parallel to the x-axis, it has an equation of  , where the focus is ( , where the focus is (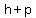 , ,  ) and the directrix is ) and the directrix is . .
The "general" form of equation of a parabola is the one you're used to,  unless the quadratic is "sideways", in which case the equation will look something like unless the quadratic is "sideways", in which case the equation will look something like  . .
vertex as ( , , )=> )=> , , 
directrix of 
it has an equation of 


we need to find  , using the directrix is , using the directrix is and vertex and vertex
if given directrix of  and and  , then , then




 ->The standard form ->The standard form
the "general" form of equation:
 .......solve for .......solve for 



 -> the general form -> the general form

|
|
|
| |