SOLUTION: Find the equation of the tangent to {{{y=1/(x-4)}}} that passes through the origin.

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find the equation of the tangent to {{{y=1/(x-4)}}} that passes through the origin.      Log On


   

Question 1151169: Find the equation of the tangent to y=1%2F%28x-4%29 that passes through the origin.
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


An arbitrary point on the graph of the function is (a,1/(a-4)).

We need to have the slope of the line containing (0,0) and (a,1/(a-4) equal to the slope of the graph of y=1/(x-4) at x=a -- that is, equal to the derivative of the function at x=a.

y+=+1%2F%28x-4%29+=+%28x-4%29%5E%28-1%29
dy%2Fdx+=+-%28x-4%29%5E%28-2%29+=+-1%2F%28x-4%29%5E2

The derivative at x=a is

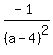
%28-1%29%2F%28a-4%29%5E2

The slope of the line containing (0,0) and (a,1/(a-4) is

%281%2F%28a-4%29%29%2Fa+=+1%2F%28a%5E2-4a%29

So

1%2F%28a%5E2-4a%29+=+%28-1%29%2F%28a-4%29%5E2
%28a-4%29%5E2+=+-1%28a%5E2-4a%29
a%5E2-8a%2B16+=+-a%5E2%2B4a
2a%5E2-12a%2B16+=+0
a%5E2-6a%2B8+=+0
%28a-2%29%28a-4%29+=+0
a+=+2 or a+=+4

The function is undefined at x=4; so our solution should be at x=2.

For x=2, the point on the graph is (2,1/(2-4)) = (2,-1/2).

The line through (0,0) and (2,-1/2) -- and therefore the tangent line we are looking for -- is y = (-1/4)x.

A graph of the function and the tangent line through the origin:

graph%28400%2C400%2C-2%2C5%2C-1%2C1%2C1%2F%28x-4%29%2C-%281%2F4%29x%29