Question 1149990: Write an equation for the hyperbola that has eccentricity 3, center at (0,0), and vertex at (0,8)
An equation for the hyperbola is...?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! the hyperbola has a horizontal transverse axis and its standard form of the equation is:

the hyperbola has a vertical transverse axis and its standard form of the equation is:

( , , ) is the center ) is the center
 is the distance between is the distance between  and and  , the length of the transverse axis is , the length of the transverse axis is 
the length of the conjugate axis is 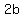
 is the distance between is the distance between 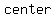 and and 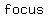

The 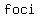 of the hyperbola is ( of the hyperbola is ( , , ± ±  ). ).
The  of the hyperbola is ( of the hyperbola is ( , , ± ±  ). ).
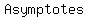 of the hyperbola are: of the hyperbola are: 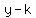 = ± = ±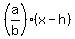 . .
The formula for   is: is: 
given:
the hyperbola that has eccentricity  , => , =>
center at ( , , ), => ), => , , and your formula becomes and your formula becomes
 (the standard equation for a hyperbola with a vertical transverse axis) (the standard equation for a hyperbola with a vertical transverse axis)
vertex at ( , , )=> )=> 
then  ........solve for ........solve for 
 .......square both sides .......square both sides




and, your formula is: 

|
|
|