Question 1149989: Find the standard form of the equation of the hyperbola satisfying the given conditions.
x-intercepts (0,24) and (0,-24). foci at (-26,0) and (26,0)
The equation in standard form of the hyperbola is..
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
the hyperbola satisfying the given conditions
x-intercepts ( , , ) and ( ) and ( , , ) => ) => , these are , these are 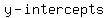
the hyperbola has a vertical transverse axis and its standard form of the equation is:

foci at (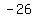 , , ) and ( ) and (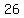 , , )=>The center lies on the x-axis and center is at ( )=>The center lies on the x-axis and center is at ( , , ) )
then, your formula is 
The distance from the center point to one focus is called  and can be found using this formula: and can be found using this formula:
 => since => since 


use y-intercept ( , , ) and ) and  , plug in , plug in

 .......solve for .......solve for 





find  : :


and, your formula is: 

|
|
|