|
Question 1144228: Determine the general equation of the ellipse with center (0,0), a focus of (0, √7), and a vertex of (0,4).
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The center is at (0,0), and the coordinates of the vertex and focus tell us the major axis is vertical. The general equation is then
 [1] [1]
where a is the semi-major axis and b is the semi-minor axis.
The distance from the center to each focus is c, where a, b, and c are related by
 [2] [2]
The given coordinates of a focus and a vertex tell us c = sqrt(7) and a = 4.
Use those values in [2] to determine the value of a; then write the equation [1] using the values of a and b.
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The post by @greenestamps has some typos.
So I came to fix them and to present a clean solution.
The center is at (0,0), and the coordinates of the vertex and focus tell us the major axis is vertical.
It means that the ellipse is TALLER than WIDE. The general equation is then
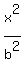 + + 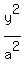 = 1 (1)
where a is the semi-major axis and b is the semi-minor axis.
Notice that the major semi-axis "a" is associated with y-term in equation (1): it is because the ellipse is TALLER than WIDE.
The distance from the center to each focus is c, where a, b, and c are related by = 1 (1)
where a is the semi-major axis and b is the semi-minor axis.
Notice that the major semi-axis "a" is associated with y-term in equation (1): it is because the ellipse is TALLER than WIDE.
The distance from the center to each focus is c, where a, b, and c are related by
 = =  - -  (2) ( <<<---=== it is the line where I fixed the typo (!) )
The given coordinates of a focus and a vertex tell us c = sqrt(7) and a = 4.
Therefore, (2) ( <<<---=== it is the line where I fixed the typo (!) )
The given coordinates of a focus and a vertex tell us c = sqrt(7) and a = 4.
Therefore,  = =  - -  = =  - - 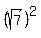 = 16 - 7 = 9 and b = = 16 - 7 = 9 and b =  = 3.
Thus the final equation of this ellipse is = 3.
Thus the final equation of this ellipse is
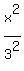 + + 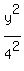 = 1,
or = 1,
or
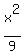 + + 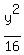 = 1. = 1.
Completed and solved.
--------------------
This reference might be useful to you
- Ellipse definition, canonical equation, characteristic points and elements
It is my lesson in this site, which contains all relevant formulas related to ellipses.
|
|
|
| |