Question 1144012: Find the equation of the hyperbola with the following properties.
Foci at (-8,-7) and (-8,-13)
Vertices at (-8,-9) and (-8,-11)
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) Foci at (-8,-7) and (-8,-13)
So...
Transverse axis is vertical
General equation is 
c = 3
center (h,k) = (-8,-10)
(2) Vertices at (-8,-9) and (-8,-11)
So a = 1.
Use c^2 = a^2+b^2 to determine b^2; then write the equation.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equation of the hyperbola with the following properties.
Foci at (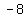 ) and ( ) and ( , , ) )
Vertices at ( , , ) and ( ) and ( , , ) )
recall: ( , , ), which is the "center" of the hyperbola. ), which is the "center" of the hyperbola.
The point on each branch closest to the center is that branch's "vertex". The vertices are some fixed distance  from the center. from the center.
The "foci" of an hyperbola are "inside" each branch, and each focus is located some fixed distance  from the center. from the center.
Take note that ALL of the points given to you (both vertices and foci) all have a x-coordinate of  . So this tells us that the hyperbola opens . So this tells us that the hyperbola opens 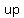 and and  and has a form and has a form
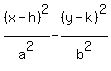
So we need to find the values of  , ,  , ,  , and , and  . .
Now let's find the midpoint of the line connecting the vertices. This midpoint is the center of the hyperbola.
 mid=Average the mid=Average the  -coordinates of the vertices -coordinates of the vertices
 mid=Average the mid=Average the  -coordinates of the vertices -coordinates of the vertices
so, ( , ,  )=( )=(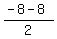 , , 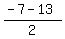 )=( )=( , , ) )
=> , , 
and center is at ( , ,  )=( )=( , ,  ) )
If the  term has the minus sign then the hyperbola will open up and down. term has the minus sign then the hyperbola will open up and down.
if vertices at ( , , ) and ( ) and ( , , ) on same vertical line, hyperbola opens up and down ) on same vertical line, hyperbola opens up and down
and
we know that vertices are at:
( , ,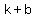 )=( )=( , , )....since )....since  , ,  , solve for , solve for 
( , ,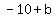 )=( )=( , , )=> )=> => => => =>
and same for other vertices
( , ,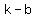 )=( )=( , , ) )
( , ,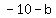 )=( )=(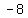 ) => ) => => => => =>
so far we know that:
 (distance from vertex to center) (distance from vertex to center)
 (distance from focus to center) (distance from focus to center)
now find 




so, your hyperbola open up and down and it is:



|
|
|